예제: 극한 연산자 사용
극한 값으로 무한대 사용
1. 식의 인수가 무한대에 접근할 경우 극한 연산자를 사용하여 식을 기호로 연산합니다.
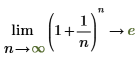
2. 시각화의 편의를 위해 함수를 도표화합니다. 가로 마커를 사용하여 e를 표시합니다.
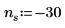 | 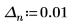 | 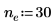 |
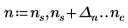 | ||
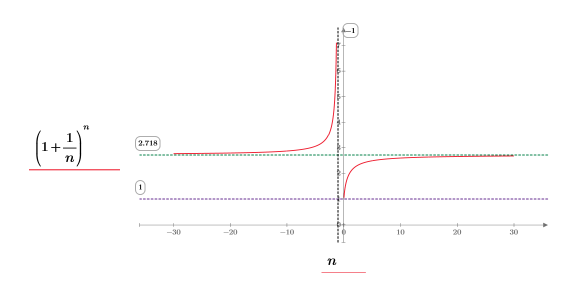 | ||
(x, y)사분에서 다음을 관찰합니다.
◦ n이 positive infinity에 접근하면 함수가 y=e에 접근합니다.
◦ n이 0에 접근하면 함수가 y=1에 접근합니다.
수학적으로는 다음과 같은 기호 연산으로 표현됩니다.
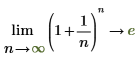 | 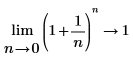 |
(-x, y)사분에서 다음을 관찰합니다.
◦ n이 negative infinity에 접근하면 함수가 y=e에 접근합니다.
◦ n이 -1에 접근하면 함수가 y=infinity에 접근합니다.
수학적으로는 다음과 같은 기호 연산으로 표현됩니다.
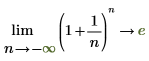 | 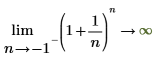 |
두 번째 방정식의 좌변에 사용된 극한 방향은 -1이 곡선의 왼쪽에서 접근한다는 의미입니다. 지정하지 않으면 -1 < n < 0에 대한 함수가 정의되지 않기 때문에 연산이 "정의되지 않음"을 반환합니다. 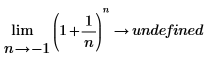 |
극한 방향 사용
1. cot 함수를 도표화합니다.
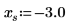 | 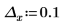 | 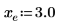 |
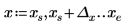 | ||
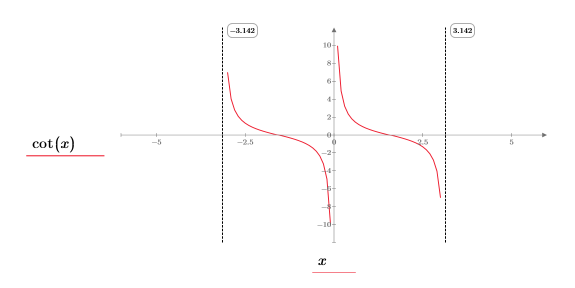 | ||
(x, y)사분에서 다음을 관찰합니다.
◦ x이 0에 접근하면 함수가 y=infinity에 접근합니다.
◦ x이 π에 접근하면 함수가 y=-infinity에 접근합니다.
수학적으로는 다음과 같은 기호 연산으로 표현됩니다.
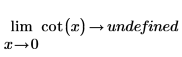 | 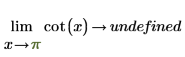 |
함수가 x=+/- n*π/2를 중심으로 대칭이기 때문에 기호 연산은 "정의되지 않음"을 반환합니다. 이는 x=0(및 π의 모든 배수) 위치에서 x가 0에 접근하는 방향에 따라 함수가 infinity 또는 -infinity이기 때문입니다.
이 경우 "극한 방향"을 지정하는 것이 좋습니다.
2. "극한 방향"을 지정하고 cot 함수를 0 및 π에서 기호 연산으로 계산합니다.
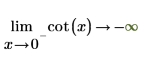 | 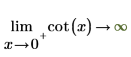 |
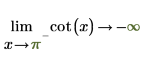 | 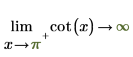 |
반환된 결과가 도표와 일치합니다.
함수를 시각화하고 기호 연산 결과의 유효성을 확인할 수 있도록 함수를 도표화하는 것이 도움이 됩니다. |