예제: 방정식의 기호 해

기호 > 기호 연산 > 예제: 방정식의 기호 해

예제: 방정식의 기호 해

하나 이상의 미지수가 있는 방정식을 기호 연산으로 풉니다.

단일 방정식 풀이

1. 다음 방정식을 입력합니다.

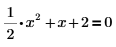
2. 기호 연산 연산자를 삽입하고 자리 표시자에 solve 키워드를 입력한 다음 Enter 키를 누릅니다.

<region id="ID0EE2PKB" actualWidth="247.93600031296413" actualHeight="56.690667054653176" top="96.000000000000014" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="28">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <mult />
            <apply>
              <div />
              <real>1</real>
              <real>2</real>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve">x</id>
              <real>2</real>
            </apply>
          </apply>
          <id xml:space="preserve">x</id>
        </apply>
        <real>2</real>
      </apply>
      <command>
        <id xml:space="preserve">solve</id>
      </command>
      <symResult>
        <matrix rows="2" cols="1">
          <apply>
            <minus />
            <apply>
              <mult />
              <apply>
                <nthRoot />
                <placeholder />
                <real>3</real>
              </apply>
              <imag symbol="i">1</imag>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <minus />
            <apply>
              <neg />
              <parens>
                <apply>
                  <mult />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <real>3</real>
                  </apply>
                  <imag symbol="i">1</imag>
                </apply>
              </parens>
            </apply>
            <real>1</real>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

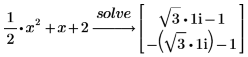
방정식의 우변이 0이므로 식의 =0 부분을 입력할 필요가 없습니다.

3. 상수 2를 소수 형식 2.0으로 입력하여 해를 부동소수점 형식으로 구합니다.

<region id="ID0ET4PKB" actualWidth="384.61" actualHeight="51.158666666666669" top="172.80000000000004" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="29">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <mult />
            <apply>
              <div />
              <real>1</real>
              <real>2</real>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve">x</id>
              <real>2</real>
            </apply>
          </apply>
          <id xml:space="preserve">x</id>
        </apply>
        <real>2.0</real>
      </apply>
      <command>
        <id xml:space="preserve">solve</id>
      </command>
      <symResult>
        <matrix rows="2" cols="1">
          <apply>
            <plus />
            <real>-1.0</real>
            <imag symbol="i">1.7320508075688772935</imag>
          </apply>
          <apply>
            <minus />
            <real>-1.0</real>
            <imag symbol="i">1.7320508075688772935</imag>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

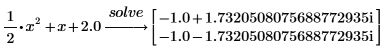
4. 변수 하나가 있는 방정식을 풉니다.

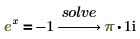
5. 여러 개의 변수가 있는 방정식을 풉니다.

<region id="ID0ETAQKB" actualWidth="230.36333333333334" actualHeight="53.31066666666667" top="326.4" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="31">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <div />
          <apply>
            <plus />
            <apply>
              <mult />
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">α</id>
              <id xml:space="preserve">f</id>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <minus />
            <id xml:space="preserve">f</id>
            <id xml:space="preserve">β</id>
          </apply>
        </apply>
        <apply>
          <pow />
          <id xml:space="preserve" labels="CONSTANT">e</id>
          <apply>
            <neg />
            <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">α</id>
          </apply>
        </apply>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">solve</id>
          <id xml:space="preserve">f</id>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <plus />
            <apply>
              <mult />
              <id xml:space="preserve" labels="VARIABLE">β</id>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <neg />
                  <id xml:space="preserve" labels="VARIABLE">α</id>
                </apply>
              </apply>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <minus />
            <apply>
              <pow />
              <id xml:space="preserve" labels="CONSTANT">e</id>
              <apply>
                <neg />
                <id xml:space="preserve" labels="VARIABLE">α</id>
              </apply>
            </apply>
            <id xml:space="preserve" labels="VARIABLE">α</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

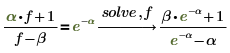
방정식에 여러 개의 변수가 있는 경우 풀이할 변수를 지정해야 합니다.

6. 4차 다항식을 풉니다.

<region id="ID0E4CQKB" actualWidth="656.99666666666667" actualHeight="81.4" top="422.40000000000009" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="32">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <plus />
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>4</real>
              </apply>
              <apply>
                <mult />
                <real>3</real>
                <apply>
                  <pow />
                  <id xml:space="preserve">x</id>
                  <real>3</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <real>17.2</real>
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>2</real>
              </apply>
            </apply>
          </apply>
          <apply>
            <mult />
            <real>3</real>
            <id xml:space="preserve">x</id>
          </apply>
        </apply>
        <real>60.5</real>
      </apply>
      <command>
        <id xml:space="preserve">solve</id>
      </command>
      <symResult>
        <matrix rows="4" cols="1">
          <apply>
            <plus />
            <real>1.8446429879763482325</real>
            <imag symbol="i">3.5421915825432999263</imag>
          </apply>
          <apply>
            <minus />
            <real>1.8446429879763482325</real>
            <imag symbol="i">3.5421915825432999263</imag>
          </apply>
          <apply>
            <plus />
            <real>-0.34464298797634823247</real>
            <imag symbol="i">1.9168634105775423629</imag>
          </apply>
          <apply>
            <minus />
            <real>-0.34464298797634823247</real>
            <imag symbol="i">1.9168634105775423629</imag>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

위 결과에서는 4차 다항식의 기호 해로 4개의 수치 해를 산출하는 것을 보여줍니다.

7. 매개변수화된 계수를 사용하여 다항식의 근을 구합니다.

<region id="ID0E6GQKB" actualWidth="222.79266697963081" actualHeight="118.49066705465319" top="633.60000000000014" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="37">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">f</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">solve</id>
          <id xml:space="preserve">x</id>
        </sequence>
      </command>
      <symResult>
        <matrix rows="3" cols="1">
          <real>-1</real>
          <apply>
            <div />
            <apply>
              <plus />
              <apply>
                <mult />
                <apply>
                  <nthRoot />
                  <placeholder />
                  <real>11</real>
                </apply>
                <imag symbol="i">1</imag>
              </apply>
              <real>1</real>
            </apply>
            <real>2</real>
          </apply>
          <apply>
            <div />
            <apply>
              <plus />
              <apply>
                <neg />
                <parens>
                  <apply>
                    <mult />
                    <apply>
                      <nthRoot />
                      <placeholder />
                      <real>11</real>
                    </apply>
                    <imag symbol="i">1</imag>
                  </apply>
                </parens>
              </apply>
              <real>1</real>
            </apply>
            <real>2</real>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

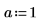
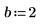
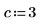
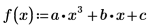
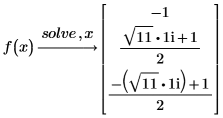
방정식 및 등식 시스템 풀이

여러 방정식과 등식을 벡터로 그룹화하여 단일 방정식 시스템으로 함께 풀어낼 수 있습니다.

<region id="ID0E2HQKB" actualWidth="339.94800093889239" actualHeight="170.98080162954329" top="806.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="38">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <matrix rows="2" cols="1">
        <apply>
          <equal />
          <apply>
            <plus />
            <id xml:space="preserve">x</id>
            <apply>
              <pow />
              <id xml:space="preserve">y</id>
              <real>2</real>
            </apply>
          </apply>
          <real>3</real>
        </apply>
        <apply>
          <equal />
          <apply>
            <plus />
            <apply>
              <pow />
              <id xml:space="preserve">x</id>
              <real>3</real>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve">y</id>
              <real>4</real>
            </apply>
          </apply>
          <real>5</real>
        </apply>
      </matrix>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">x</id>
          </sequence>
          <id xml:space="preserve">y</id>
        </sequence>
      </command>
      <symResult>
        <matrix rows="6" cols="2">
          <real>1</real>
          <real>1</real>
          <apply>
            <minus />
            <apply>
              <nthRoot />
              <placeholder />
              <real>5</real>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <minus />
            <apply>
              <nthRoot />
              <placeholder />
              <real>5</real>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <minus />
            <apply>
              <neg />
              <apply>
                <nthRoot />
                <placeholder />
                <real>5</real>
              </apply>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <minus />
            <apply>
              <neg />
              <apply>
                <nthRoot />
                <placeholder />
                <real>5</real>
              </apply>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <nthRoot />
            <placeholder />
            <real>2</real>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <real>2</real>
            </apply>
          </apply>
          <apply>
            <nthRoot />
            <placeholder />
            <apply>
              <plus />
              <apply>
                <neg />
                <apply>
                  <nthRoot />
                  <placeholder />
                  <real>5</real>
                </apply>
              </apply>
              <real>4</real>
            </apply>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <neg />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <real>5</real>
                  </apply>
                </apply>
                <real>4</real>
              </apply>
            </apply>
          </apply>
          <apply>
            <nthRoot />
            <placeholder />
            <apply>
              <plus />
              <apply>
                <nthRoot />
                <placeholder />
                <real>5</real>
              </apply>
              <real>4</real>
            </apply>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <nthRoot />
                  <placeholder />
                  <real>5</real>
                </apply>
                <real>4</real>
              </apply>
            </apply>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EJIQKB" actualWidth="329.19800093889239" actualHeight="67.104000000000013" top="1017.6000000000001" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="39">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <matrix rows="3" cols="1">
        <apply>
          <equal />
          <apply>
            <plus />
            <id xml:space="preserve">x</id>
            <apply>
              <pow />
              <id xml:space="preserve">y</id>
              <real>2</real>
            </apply>
          </apply>
          <real>3</real>
        </apply>
        <apply>
          <equal />
          <apply>
            <plus />
            <apply>
              <pow />
              <id xml:space="preserve">x</id>
              <real>3</real>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve">y</id>
              <real>4</real>
            </apply>
          </apply>
          <real>5</real>
        </apply>
        <apply>
          <greaterThan />
          <id xml:space="preserve">x</id>
          <id xml:space="preserve">y</id>
        </apply>
      </matrix>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">x</id>
          </sequence>
          <id xml:space="preserve">y</id>
        </sequence>
      </command>
      <symResult>
        <matrix rows="2" cols="2">
          <real>1</real>
          <apply>
            <minus />
            <apply>
              <nthRoot />
              <placeholder />
              <real>5</real>
            </apply>
            <real>1</real>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <real>2</real>
            </apply>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <neg />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <real>5</real>
                  </apply>
                </apply>
                <real>4</real>
              </apply>
            </apply>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

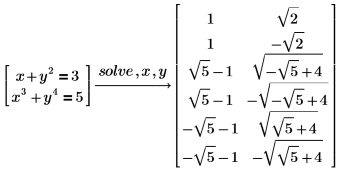
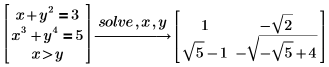
라디칼로 다항식 풀이

기본적으로 PTC Mathcad에서는 최대 4차까지 다항식 방정식을 라디칼로 풉니다. 일반 산술 연산을 사용하여 해가 라디칼로 작성됩니다.

1. 다음 다항식을 풉니다.

<region id="ID0EVKQKB" actualWidth="309.39133427222572" actualHeight="207.69013457489015" top="1190.4" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="40">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <pow />
            <id xml:space="preserve">x</id>
            <real>4</real>
          </apply>
          <apply>
            <pow />
            <id xml:space="preserve">x</id>
            <real>2</real>
          </apply>
        </apply>
        <real>1</real>
      </apply>
      <command>
        <id xml:space="preserve">solve</id>
      </command>
      <symResult>
        <matrix rows="4" cols="1">
          <apply>
            <div />
            <apply>
              <mult />
              <apply>
                <nthRoot />
                <placeholder />
                <real>2</real>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <apply>
                      <nthRoot />
                      <placeholder />
                      <real>3</real>
                    </apply>
                    <imag symbol="i">1</imag>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
            <real>2</real>
          </apply>
          <apply>
            <div />
            <apply>
              <neg />
              <parens>
                <apply>
                  <mult />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <real>2</real>
                  </apply>
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <plus />
                      <apply>
                        <mult />
                        <apply>
                          <nthRoot />
                          <placeholder />
                          <real>3</real>
                        </apply>
                        <imag symbol="i">1</imag>
                      </apply>
                      <real>1</real>
                    </apply>
                  </apply>
                </apply>
              </parens>
            </apply>
            <real>2</real>
          </apply>
          <apply>
            <div />
            <apply>
              <mult />
              <apply>
                <nthRoot />
                <placeholder />
                <real>2</real>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <apply>
                          <nthRoot />
                          <placeholder />
                          <real>3</real>
                        </apply>
                        <imag symbol="i">1</imag>
                      </apply>
                    </parens>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
            <real>2</real>
          </apply>
          <apply>
            <div />
            <apply>
              <neg />
              <parens>
                <apply>
                  <mult />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <real>2</real>
                  </apply>
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <plus />
                      <apply>
                        <neg />
                        <parens>
                          <apply>
                            <mult />
                            <apply>
                              <nthRoot />
                              <placeholder />
                              <real>3</real>
                            </apply>
                            <imag symbol="i">1</imag>
                          </apply>
                        </parens>
                      </apply>
                      <real>1</real>
                    </apply>
                  </apply>
                </apply>
              </parens>
            </apply>
            <real>2</real>
          </apply>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

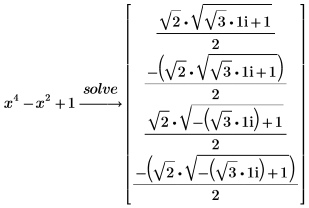
19세기에 수학자 갈르와는 라디칼로 풀 수 없는 5차 이상의 다항식이 있음을 증명했습니다. 이러한 다항식의 경우 PTC Mathcad에서는 근의 수치적 근사화를 구합니다.

2. 5차 다항식을 풉니다.

<region id="ID0ELNQKB" actualWidth="535.01" actualHeight="100" top="1363.2000000000003" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="41">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <minus />
          <apply>
            <pow />
            <id xml:space="preserve">x</id>
            <real>5</real>
          </apply>
          <apply>
            <mult />
            <real>10</real>
            <id xml:space="preserve">x</id>
          </apply>
        </apply>
        <real>2</real>
      </apply>
      <command>
        <id xml:space="preserve">solve</id>
      </command>
      <symResult>
        <matrix rows="5" cols="1">
          <real>-1.8251134808337678023</real>
          <apply>
            <minus />
            <real>-0.049612509519204534977</real>
            <imag symbol="i">1.7817417950586724694</imag>
          </apply>
          <apply>
            <plus />
            <real>-0.049612509519204534977</real>
            <imag symbol="i">1.7817417950586724694</imag>
          </apply>
          <real>0.20003202562870940866</real>
          <real>1.7243064742434674636</real>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

위 결과에서는 5차 다항식의 기호 해로 5개의 수치 해를 산출하는 것을 보여줍니다.

변수 정의역에 대한 가정 세우기

assume 키워드를 사용하여 문제의 변수 정의역에 대한 가정을 세울 수 있습니다. 예를 들어 정의역이 실수라고 가정합니다.

1. x가 실수라고 가정하여 방정식을 풉니다.

<region id="ID0EKQQKB" actualWidth="361.00933364629748" actualHeight="75.29066705465317" top="1478.4000000000003" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="42">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <mult />
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>3</real>
              </apply>
              <real>1</real>
            </apply>
          </parens>
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>2</real>
              </apply>
              <real>2</real>
            </apply>
          </parens>
        </apply>
        <real>0</real>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">assume</id>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">x</id>
            <id xml:space="preserve">real</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <matrix rows="3" cols="1">
          <apply>
            <nthRoot />
            <placeholder />
            <real>2</real>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <real>2</real>
            </apply>
          </apply>
          <real>1</real>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

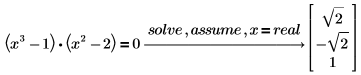
PTC Mathcad에서 방정식에 대한 실수 해만 구합니다.

2. RealRange를 사용하여 (0, 2) 범위에서 실수 해를 구합니다.

<region id="ID0EGTQKB" actualWidth="436.9626669796308" actualHeight="52.6126667636633" top="1555.2000000000003" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="43">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <mult />
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>3</real>
              </apply>
              <real>1</real>
            </apply>
          </parens>
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>2</real>
              </apply>
              <real>2</real>
            </apply>
          </parens>
        </apply>
        <real>0</real>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">assume</id>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">x</id>
            <apply>
              <id xml:space="preserve">RealRange</id>
              <sequence>
                <real>0</real>
                <real>2</real>
              </sequence>
            </apply>
          </apply>
        </sequence>
      </command>
      <symResult>
        <matrix rows="2" cols="1">
          <apply>
            <nthRoot />
            <placeholder />
            <real>2</real>
          </apply>
          <real>1</real>
        </matrix>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

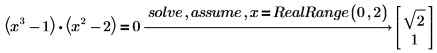
3. 정수 해만 구하려면 x=integer를 입력합니다.

<region id="ID0E1UQKB" actualWidth="342.99666666666667" actualHeight="39.2" top="1612.8000000000002" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="44">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <mult />
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>3</real>
              </apply>
              <real>1</real>
            </apply>
          </parens>
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>2</real>
              </apply>
              <real>2</real>
            </apply>
          </parens>
        </apply>
        <real>0</real>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">assume</id>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">x</id>
            <id xml:space="preserve">integer</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <real>1</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

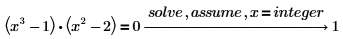
4. 기호 연산에서 변수의 정의역을 제한하려면 assume을 사용합니다.

<region id="ID0E3WQKB" actualWidth="227.24333333333334" actualHeight="57.800000000000004" top="1747.2000000000003" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="46">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
        <apply>
          <mult />
          <id xml:space="preserve" labels="CONSTANT">π</id>
          <id xml:space="preserve">n</id>
        </apply>
      </apply>
      <command>
        <id xml:space="preserve">simplify</id>
      </command>
      <command>
        <sequence>
          <id xml:space="preserve">assume</id>
          <apply>
            <equal />
            <id xml:space="preserve">n</id>
            <id xml:space="preserve">integer</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <real>0</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

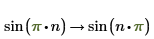
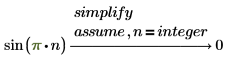
방정식에 대한 자세한 해 구하기

solve 다음에 fully 수정자를 추가하여 방정식에 대해 자세한 해를 구합니다.

1. clear.sym 함수를 사용하여 a의 이전 기호 값을 지웁니다.

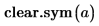
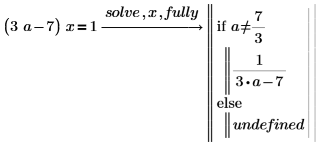
2. fully를 사용하여 해가 유효한 a의 값을 구합니다.

<region id="ID0E51QKB" actualWidth="320.72" actualHeight="145.60000000000002" top="1881.6000000000004" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <scale />
          <parens>
            <apply>
              <minus />
              <apply>
                <scale />
                <real>3</real>
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
              </apply>
              <real>7</real>
            </apply>
          </parens>
          <id xml:space="preserve">x</id>
        </apply>
        <real>1</real>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">x</id>
          </sequence>
          <id xml:space="preserve">fully</id>
        </sequence>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <notEqual />
                <id xml:space="preserve" labels="VARIABLE">a</id>
                <apply>
                  <div />
                  <real>7</real>
                  <real>3</real>
                </apply>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <real>1</real>
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <real>3</real>
                      <id xml:space="preserve" labels="VARIABLE">a</id>
                    </apply>
                    <real>7</real>
                  </apply>
                </apply>
              </program>
            </then>
            <else>
              <program>
                <id xml:space="preserve" labels="*">undefined</id>
              </program>
            </else>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

3. 자세한 결과를 사용하여 함수를 정의합니다.

<region id="ID0EO3QKB" actualWidth="371.95333333333338" actualHeight="145.60000000000002" top="2054.4" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="49">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id xml:space="preserve" labels="FUNCTION">f</id>
        <boundVars>
          <id xml:space="preserve" labels="VARIABLE">a</id>
        </boundVars>
      </function>
      <symEval>
        <apply>
          <equal />
          <apply>
            <mult />
            <parens>
              <apply>
                <minus />
                <apply>
                  <mult />
                  <real>3</real>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
                </apply>
                <real>7</real>
              </apply>
            </parens>
            <id xml:space="preserve">x</id>
          </apply>
          <real>1</real>
        </apply>
        <command>
          <sequence>
            <sequence>
              <id xml:space="preserve">solve</id>
              <id xml:space="preserve">x</id>
            </sequence>
            <id xml:space="preserve">fully</id>
          </sequence>
        </command>
        <symResult>
          <program>
            <if>
              <test>
                <apply>
                  <notEqual />
                  <id xml:space="preserve" labels="VARIABLE">a</id>
                  <apply>
                    <div />
                    <real>7</real>
                    <real>3</real>
                  </apply>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <div />
                    <real>1</real>
                    <apply>
                      <minus />
                      <apply>
                        <mult />
                        <real>3</real>
                        <id xml:space="preserve" labels="VARIABLE">a</id>
                      </apply>
                      <real>7</real>
                    </apply>
                  </apply>
                </program>
              </then>
              <else>
                <program>
                  <id xml:space="preserve" labels="*">undefined</id>
                </program>
              </else>
            </if>
          </program>
        </symResult>
      </symEval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

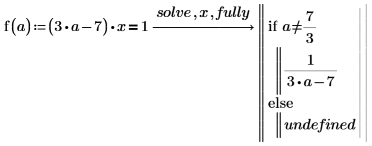
4. a=3 및 a=7/3에서 함수를 계산합니다.

주기 해가 있는 방정식

해가 주기적인 방정식의 경우 PTC Mathcad에서는 단일 해를 구한 다음 첫 번째 해에 주기의 정수 배수를 더하는 식을 구합니다.

1. fully를 사용하여 sin(x)를 계산합니다.

<region id="ID0EHBRKB" actualWidth="333.37666666666667" actualHeight="133.60000000000002" top="2323.2000000000003" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
          <id xml:space="preserve">x</id>
        </apply>
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">cos</id>
          <id xml:space="preserve">x</id>
        </apply>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">solve</id>
          <id xml:space="preserve">fully</id>
        </sequence>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <elementOf />
                <id xml:space="preserve" labels="VARIABLE">_n</id>
                <id xml:space="preserve" labels="CONSTANT">?</id>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <real>4</real>
                          <id xml:space="preserve" labels="VARIABLE">_n</id>
                        </apply>
                        <real>1</real>
                      </apply>
                    </parens>
                    <id xml:space="preserve" labels="CONSTANT">π</id>
                  </apply>
                  <real>4</real>
                </apply>
              </program>
            </then>
            <else>
              <program>
                <id xml:space="preserve" labels="*">undefined</id>
              </program>
            </else>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

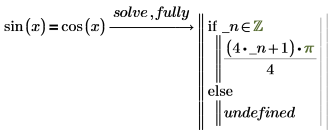
if 문 다음에 오는 식은 pi/4에 pi의 모든 정수 곱을 더한다는 의미입니다. 임의의 정수를 나타내는 새로 생성된 변수 _n이 PTC Mathcad에 삽입됩니다. 워크시트의 다른 위치에서 정의한 변수와 이름이 충돌하지 않도록 생성된 변수 앞에는 밑줄이 삽입됩니다.

2. 생성된 변수와 새 변수가 같도록 설정하는 부울 같음 연산자를 사용하여 작성된 방정식을 using 수정자 다음에 추가합니다.

<region id="ID0EJERKB" actualWidth="419.63000000000005" actualHeight="133.60000000000002" top="2476.8" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
          <id xml:space="preserve">x</id>
        </apply>
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">cos</id>
          <id xml:space="preserve">x</id>
        </apply>
      </apply>
      <command>
        <sequence>
          <sequence>
            <sequence>
              <id xml:space="preserve">solve</id>
              <id xml:space="preserve">fully</id>
            </sequence>
            <id xml:space="preserve">using</id>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">_n</id>
            <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">k</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <elementOf />
                <id xml:space="preserve" labels="VARIABLE">k</id>
                <id xml:space="preserve" labels="CONSTANT">?</id>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <real>4</real>
                          <id xml:space="preserve" labels="VARIABLE">k</id>
                        </apply>
                        <real>1</real>
                      </apply>
                    </parens>
                    <id xml:space="preserve" labels="CONSTANT">π</id>
                  </apply>
                  <real>4</real>
                </apply>
              </program>
            </then>
            <else>
              <program>
                <id xml:space="preserve" labels="*">undefined</id>
              </program>
            </else>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

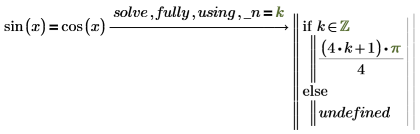
using 다음에 지정한 변수가 solve에서 구하여 생성된 변수가 아닌 경우 PTC Mathcad에서 오류가 반환됩니다.