예제: 기호 타원 적분 함수
많은 기호 계산에서 다음 타원 적분 함수가 나타납니다.
|
|
타원 적분 함수는 PTC Mathcad Prime 기본 제공 함수 집합의 일부가 아닙니다.
|
EllipticK: 제1종 완전 타원 적분
1. 제1종 완전 타원 적분 EllipticK(m)의 정의를 보여줍니다.
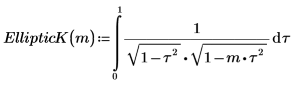
2. 수치 연산으로 EllipticK를 계산합니다.
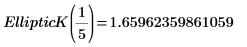
3. 0<m<1 범위에서 EllipticK이 수치 값을 도표화합니다.
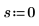 | 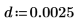 | 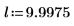 |
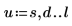 | ||
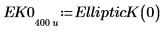 | 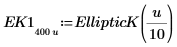 | |
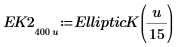 | 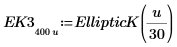 |
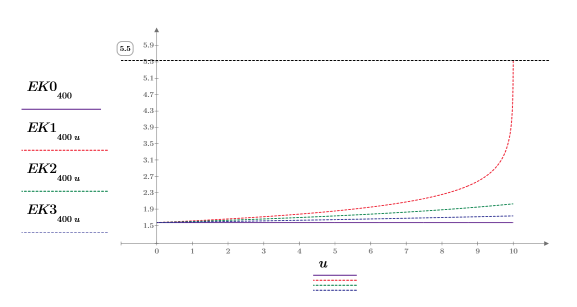
적분은 m=0일 때 π/2와 같고 m이 1에 접근할 때 12에 접근합니다. 가로 마커는 Elliptick(l/10)의 값이나 다음을 보여줍니다.
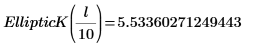
EllipticF: 제1종 불완전 타원 적분
1. 제1종 불완전 타원 적분 EllipticF(x, m)의 정의를 보여줍니다.
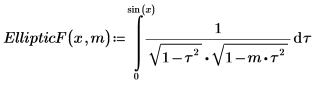
2. 수치 연산으로 EllipticF를 계산합니다.
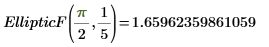
3. EllipticF와 EllipticK 간의 관계를 보여줍니다.
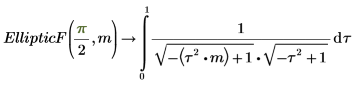
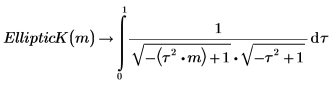
두 적분은 동일합니다.
EllipticE: 제2종 타원 적분
1. 제2종 완전 타원 적분 EllipticE(m)의 정의를 보여줍니다.
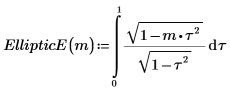
또는 함수는 다음과 같이 지정됩니다.
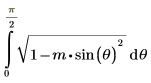
2. 수치 연산으로 EllipticE를 계산합니다.
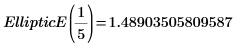
3. 제2종 불완전 타원 적분 EllipticE(x, m)의 정의를 보여줍니다.
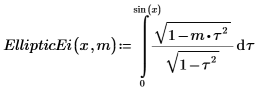
4. 수치 연산으로 EllipticEi를 계산합니다.
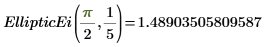
5. EllipticE와 EllipticEi 간의 관계를 보여줍니다.
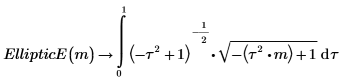
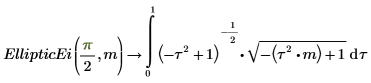
두 적분은 동일합니다.
EllipticP: 제3종 타원 적분
1. 제3종 완전 타원 적분 EllipticPi(n, m)의 정의를 보여줍니다.
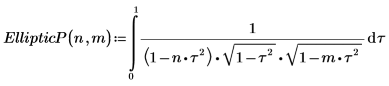
2. 수치 연산으로 EllipticP(n, m)를 계산합니다.
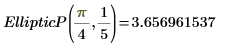
3. 제3종 불완전 타원 적분 EllipticPi(x, n, m)의 정의를 보여줍니다.
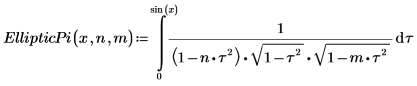
4. 수치 연산으로 EllipticPi를 계산합니다.
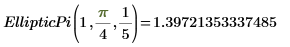
5. EllipticP와 EllipticPi 간의 관계를 보여줍니다.
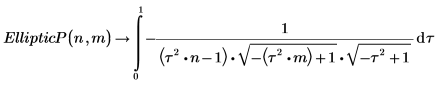
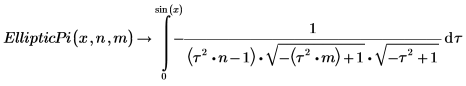
두 적분은 x=π/2에서 동일합니다.