예제: 기호 미적분 II
기호 연산 연산자를 사용하여 문제의 식을 계산하고 필요한 경우 문제를 수정하는 키워드를 추가하여 미적분에서 기호 문제를 풉니다.
테일러 및 매클로린 급수
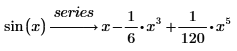
기본적으로 PTC Mathcad는 최대 6차까지의 항을 구하므로 해답의 최대 거급곱은 5입니다. |
2. series 다음에 쉼표를 입력하고 자리 표시자에 x, 10을 입력하여 항의 차수를 10으로 증가시킵니다.
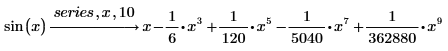
3. sin 함수를 1에 대한 테일러 급수로 전개합니다.
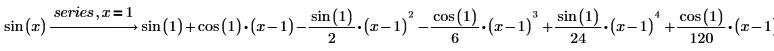
4. 함수를 점 (x, y)=(0, 1) 근처에서 여러 개의 변수로 전개합니다.
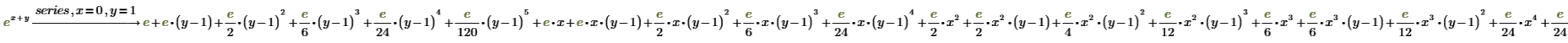
5. 계수를 e의 항이 아니라 네 자리 숫자로 표시합니다.
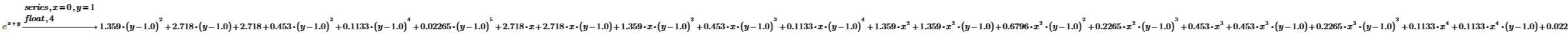
부분 분수
1. parfrac 키워드를 사용하여 유리 함수(다항식의 몫)의 부분 분수 분해를 수행합니다.
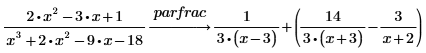
2. 범위 곱 연산자를 통해 정의된 함수의 부분 분수 분해를 수행합니다.
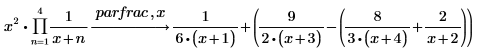
실수 또는 복소수에 대한 분해
기본적으로 PTC Mathcad는 유리수체에 대해 부분 분수 분해를 수행합니다. 즉, 초기 식이 유리 계수를 포함하는 다항식의 몫인 경우 결과의 다항식도 유리 계수를 포함합니다.
1. parfrac 키워드를 사용하여 다음 함수의 분수를 구합니다.
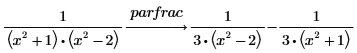
2. 다음 식의 항 중 하나에 대해 추가적인 분해를 수행합니다.
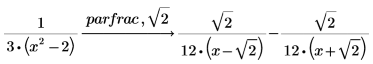
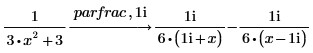
3. parfrac 다음에 domain = complex를 입력하여 복소수에 대한 유리 함수의 완전한 부분 분수 분해를 수행합니다.
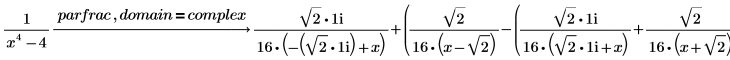
이들 단계를 반복하여 실수에 대한 분해를 수행합니다. a. 다음과 같이 simplify 키워드를 사용하여 마지막 두 항을 실수 계수가 포함된 단일 항으로 결합합니다. 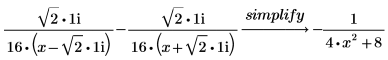 b. 원래 결과에 단순화된 결과를 대체하여 다음과 같은 결과를 얻습니다. 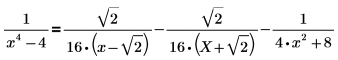 |
연분수
1. confrac 키워드를 사용하여 숫자의 연분수 전개를 구합니다.
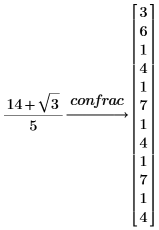
2. fraction 수정자를 사용하여 벡터가 아닌 실제 연분수를 표시합니다.
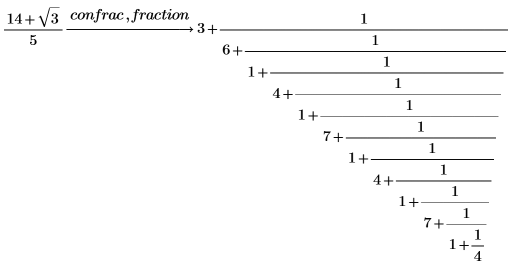
기본적으로 PTC Mathcad에서는 충분한 수의 항으로 연분수를 구하므로 해답의 정밀도가 유효 자릿수 10자리에 이릅니다. |
3. 유효 자릿수를 지정하는 양의 정수를 추가하여 결과를 다른 정밀도로 구합니다.
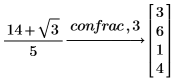

4. sin 함수를 연분수로 전개합니다.
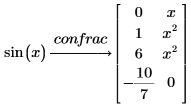
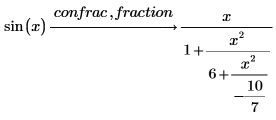
PTC Mathcad에서는 항에 해당하는 x의 거듭곱이 들어 있는 두 번째 열을 구합니다. |