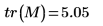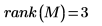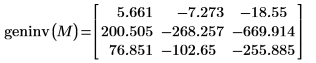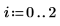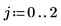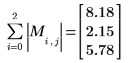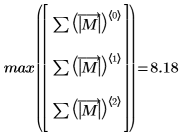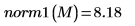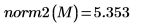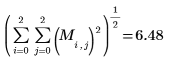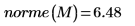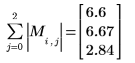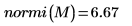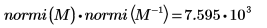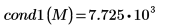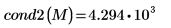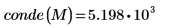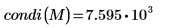예제: 특수한 특성의 행렬

벡터, 행렬 및 표 > 배열 작업 > 예제: 특수한 특성의 행렬

예제: 특수한 특성의 행렬

정방 행렬의 대각합, 순위, 일반화된 역, 놈 및 조건수를 구할 수 있습니다.

행렬의 대각합, 순위 및 일반화된 역

1. tr 함수를 사용하여 M의 대각합 즉, 대각선 요소의 합을 구합니다.

2. rank 함수를 사용하여 실수치 행렬 M의 순위를 구합니다.

3. geninv 함수를 사용하여 행렬 M의 일반화된 역을 구합니다.

행렬의 서로 다른 놈

1. M의 L1 놈(norm)을 구하고 결과를 norm1 함수의 출력과 비교합니다.

L1 놈은 절대 열 합의 최대값입니다(j= 0, 1, 2에 대해 구한 최대값).

이 식을 복사하려면 클릭

<region id="ID0ER4XGB" top="1056.0000000000002" left="19.200000000000003" height="136.00000000000003" width="191.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

2. norm2 함수를 사용하여 M의 L2 놈을 구합니다.

3. norme 함수를 사용하여 M의 유클리드 놈을 구합니다.

행렬의 유클리드 놈은 벡터의 유클리드 놈과 유사합니다.

<region id="ID0ERCYGB" top="1440.0000000000002" left="38.400000000000006" height="60.441333557128914" width="176.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="59">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <pow />
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">i</id>
              </boundVars>
              <apply>
                <summation />
                <lambda>
                  <boundVars>
                    <id xml:space="preserve">j</id>
                  </boundVars>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <indexer />
                        <id xml:space="preserve">M</id>
                        <sequence>
                          <id xml:space="preserve">i</id>
                          <id xml:space="preserve">j</id>
                        </sequence>
                      </apply>
                    </parens>
                    <real>2</real>
                  </apply>
                </lambda>
                <lowerBound>
                  <real>0</real>
                </lowerBound>
                <upperBound>
                  <real>2</real>
                </upperBound>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <real>2</real>
            </upperBound>
          </apply>
        </parens>
        <apply>
          <div />
          <real>1</real>
          <real>2</real>
        </apply>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

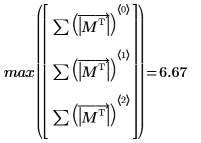
4. M의 무한 놈을 구하고 결과를 normi 함수의 출력과 비교합니다.

무한 놈은 절대 행 합의 최대값입니다(i= 0, 1, 2에 대해 구한 최대값).

이 식을 복사하려면 클릭

<region id="ID0EWFYGB" top="1766.4000000000003" left="19.200000000000003" height="143.056" width="200.52000000000004" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="65">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

행렬의 서로 다른 조건수

행렬의 조건수는 두 행렬 놈의 곱입니다. 입력 벡터에서 오차에 대한 선형 시스템 해의 민감도를 측정합니다.

1. cond1 함수를 사용하여 M의 L1 조건수를 구합니다.

2. cond2 함수를 사용하여 M의 L2 조건수를 구합니다.

3. conde 함수를 사용하여 M의 유클리드 조건수를 구합니다.

4. condi 함수를 사용하여 M의 무한 조건수를 구합니다.

관련 항목

배열을 사용한 작업 정보

도움이 되셨나요?