예제: 해 매개변수화
root 함수나 풀이 구간을 사용하여 미지의 매개변수에 따라 달라지는 방정식 또는 시스템을 푸는 함수를 정의합니다. 이렇게 하면 다양한 방정식을 풀 수 있습니다.
root 함수
매개변수 a의 값을 여러 가지로 바꾸어 방정식 f1=f2를 풉니다.
1. 두 함수를 정의합니다.
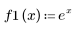
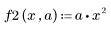
2. 새 함수 S를 정의하여 여러 a 값에 대한 방정식을 풉니다.
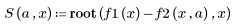
3. 초기 추측값을 정의합니다.
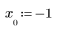
4. 매개변수 a의 범위를 정의하고 각 값에 대해 방정식을 풉니다.
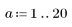
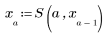
 |  | 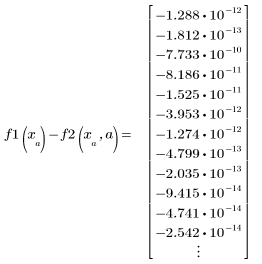 |
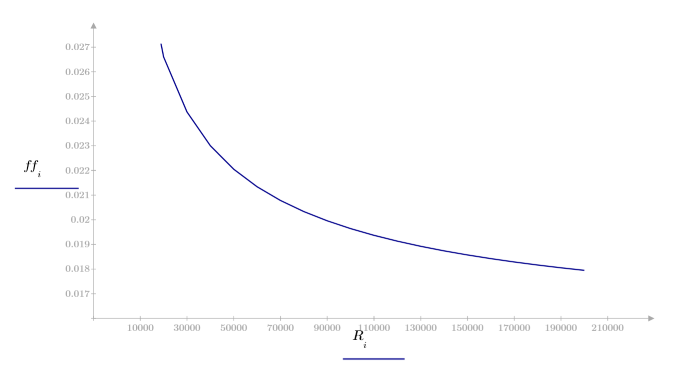
풀이 구간: 마찰 계수
지정된 값 e(파이프 거칠기), D(파이프 직경) 및 R(레이놀드 수)에 대해 마찰 계수 f를 구합니다.
1. 추측값을 정의합니다.
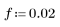
2. 풀이 구간을 작성하여 마찰 계수를 계산하는 함수를 정의합니다.

매개변수 e, D 및 R은 아직 정의되지 않았습니다. 따라서 함수 FricFac를 계산할 때마다 이 세 개의 매개변수 값을 새로 지정하여 풀이 구간을 다시 호출할 수 있습니다.
3. 다양한 레이놀드 수에 대해 마찰 계수를 계산합니다.
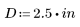
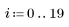
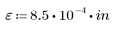
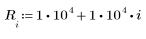
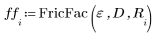
풀이 구간: 원과 선의 교차
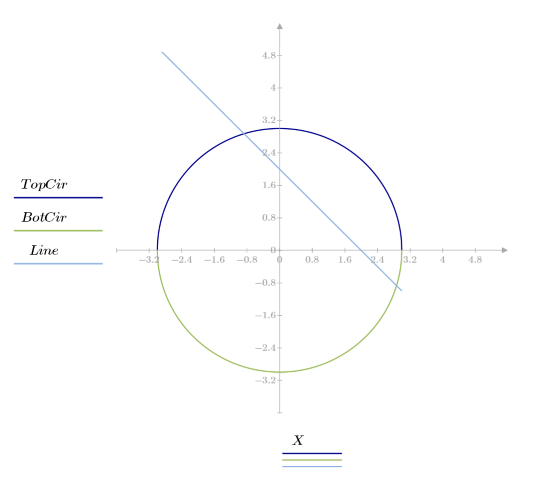
1. 원의 반경을 변경함에 따라 원과 선 y = 2 - x가 만나는 점을 구합니다.
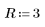
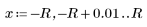
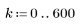
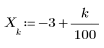
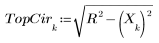
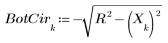
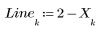
2. 풀이 구간을 작성하여 선 y = 2 - x와 반경이 R인 원의 교차점 좌표를 구하는 함수를 정의합니다.
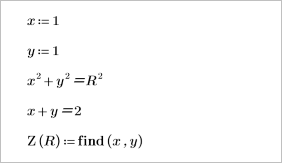
3. 새로 정의한 Z 함수를 사용하여 R=3이고 추측값 x=1 및 y=1인 경우 교차점의 좌표를 구합니다.
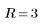
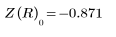
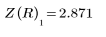
4. 교차점을 도표화합니다.
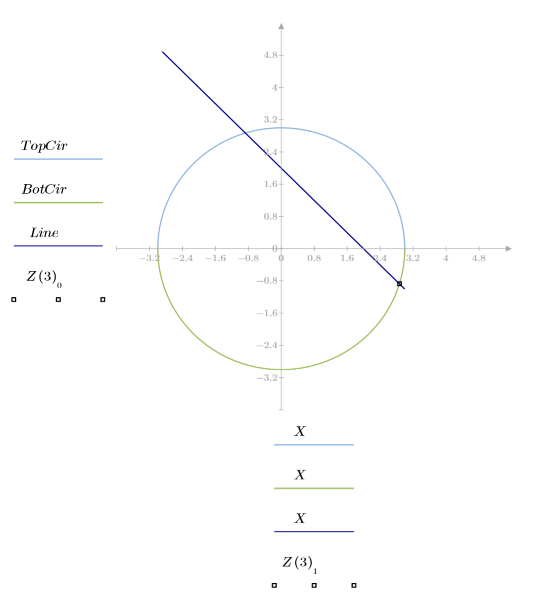
5. 새로 정의한 Z 함수를 사용하여 다섯 가지 반경 R 값에 대해 교차점 좌표를 구합니다.
 | 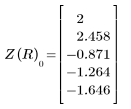 |  |
Z(R, x, y)를 정의하여 추측값에 대한 위 풀이 구간을 매개변수화할 수도 있습니다. 이렇게 풀이 구간을 매개변수화하면 풀이 구간을 하나만 설정해도 각 반경 값에 대해 2개의 해를 구할 수 있습니다.