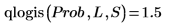예제: 몬테 카를로 확률 추정
분포를 알 수 없는 수량의 확률이 샘플링 방법으로 얼마나 크게 추정될 수 있는지를 보여 주는 난수를 생성합니다.
1. 로지스틱 분포의 위치 및 배율 매개변수를 L 및 S로 설정합니다.
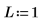
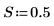
2. 몬테카를로 샘플링 매개변수를 설정합니다.
◦ 수집할 개별 표본 수:
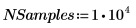
◦ 각 표본의 데이터 점 수:
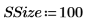
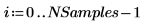
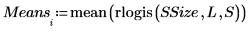
4. 난수 집합의 평균이 구간 [a, b]에 있을 확률을 추정합니다.
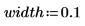
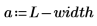
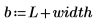
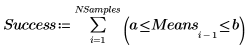
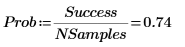
이 확률은 각 표본의 데이터 점 수와 구간의 너비에 따라 결정됩니다.
5. plogis 함수를 도표화하여 로지스틱 분포의 누적 확률 분포를 표시합니다. 가로 마커를 사용하여 확률 수준을 표시합니다.
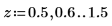
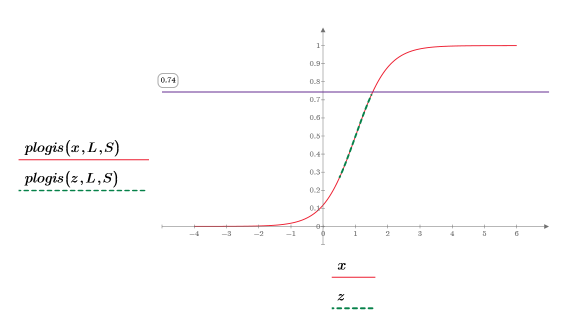
6. 도표의 녹색 파선 세그먼트를 확대하고 세로 마커를 사용하여 [a, b] 간격을 표시한 다음 가로 마커를 사용하여 [a, b] 사이의 누적 확률 하한 및 상한을 표시합니다.
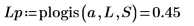
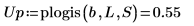
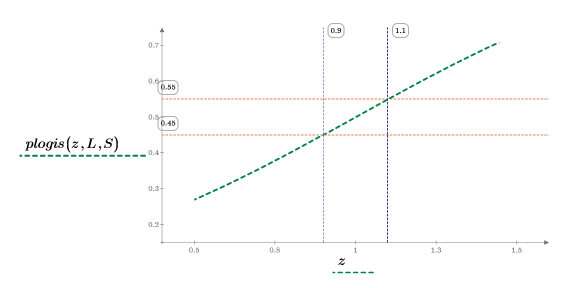
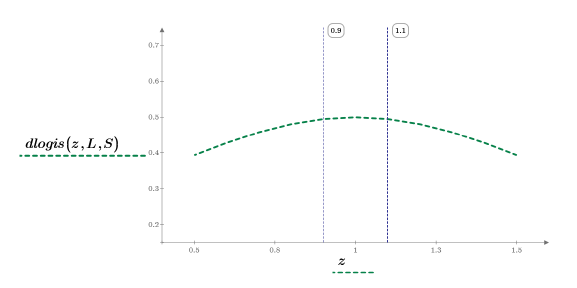
7. dlogis 함수를 도표화하여 로지스틱 분포의 확률 밀도를 표시합니다.
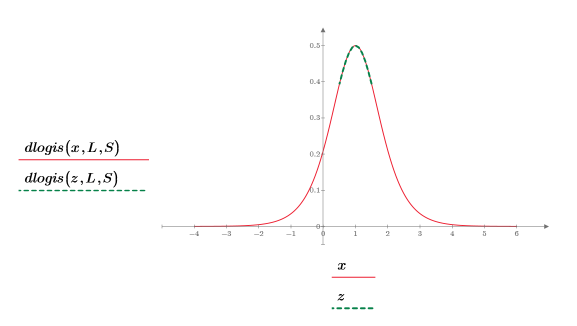
8. 도표의 녹색 파선 세그먼트를 확대하고 세로 마커를 사용하여 [a, b] 간격을 표시합니다.