예제: 복소수 행렬의 촐레스키 인수 분해

함수 > 벡터 및 행렬 > 행렬 인수 분해 > 예제: 복소수 행렬의 촐레스키 인수 분해

Cholesky 함수를 사용하여 복소수 Hermitian 행렬의 Cholesky 인수 분해를 수행합니다.

부울 비교를 수행할 때 논리적 불일치를 피하려면 계산 옵션 드롭다운 목록에서 근사 등호를 활성화합니다.

1. 복소수 Hermitian 정부호 정방 행렬 M을 정의합니다.

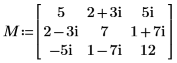
2. eigenvals 함수를 적용하여 행렬이 양의 정부호인지 확인합니다.

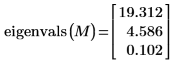
3. 주축 및 하한/상한 인수 분해의 활성화/비활성화를 제어하는 인수 p 및 u를 설정합니다.

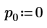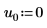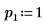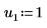4. Cholesky 함수를 사용하여 주축 및 하한 인수 분해를 포함한 행렬 M의 기본 인수 분해를 수행합니다.

기본 함수 Cholesky(M)은 Cholesky(M,1,0)과 동일합니다.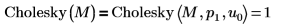

<region id="ID0E6W1EB" actualWidth="284.50666666666672" actualHeight="27.791200000000003" top="729.60000000000014" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="76">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </math>
</region>

5. P10T x M x P10 = L10 x conj(L10T)임을 보여줍니다.

<region id="ID0E5Z1EB" actualWidth="165.17000000000002" actualHeight="62.800000000000004" top="825.60000000000014" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="78"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>0</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EM11EB" actualWidth="371.56" actualHeight="62.800000000000004" top="902.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="80"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>1</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>
<region id="ID0E611EB" actualWidth="286.33333333333331" actualHeight="62.800000000000004" top="979.20000000000016" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="82"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>	<region id="ID0EN21EB" actualWidth="273.75666666666666" actualHeight="62.800000000000004" top="1056.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="84"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <conjugate /> <parens> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </parens> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>
<region id="ID0EA31EB" actualWidth="230.72333333333333" actualHeight="31.752000000000002" top="1113.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="86"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <conjugate /> <parens> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </parens> </apply> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>

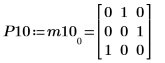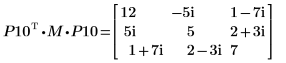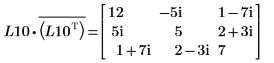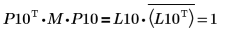관계는 논리적으로 참입니다.

6. Cholesky 함수를 사용하여 주축 및 하한 인수 분해 없이(기본값) 행렬 M의 인수 분해를 수행합니다.

<region id="ID0EE51EB" actualWidth="458.07000000000011" actualHeight="62.800000000000004" top="1248.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="88">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m00</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

Cholesky(M, 0)과 같이 인수 u를 지정하지 않으면 Cholesky(M, 0, 0)과 같이 인수를 0으로 설정하는 것과 동일합니다.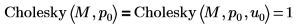

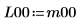
<region id="ID0E361EB" actualWidth="307.08666666666676" actualHeight="27.791200000000003" top="1344.0000000000002" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="90">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id xml:space="preserve">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

주축이 활성화된 경우 구한 하한 행렬 L10은 주축이 비활성화된 경우 구한 하한 행렬 L00과 동일하지 않습니다.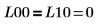

관계는 논리적으로 거짓입니다.

7. M = L00 x conj(L00T)임을 보여줍니다.

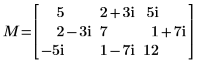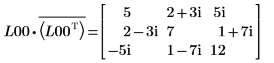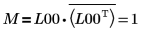관계는 논리적으로 참입니다.

8. Cholesky 함수를 사용하여 주축 및 상한 인수 분해를 포함한 행렬 M의 인수 분해를 수행합니다.

<region id="ID0E5I2EB" actualWidth="452.76666666666671" actualHeight="118.60000000000001" top="1939.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="102">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m11</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

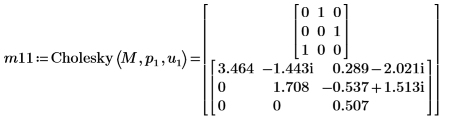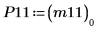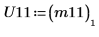9. P11T x M x P11 = conj(U11T) x U11임을 보여줍니다.

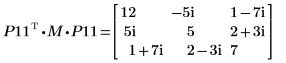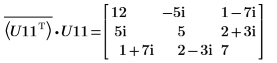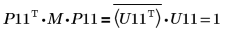관계는 논리적으로 참입니다.

10. Cholesky 함수를 사용하여 주축 및 상한 인수 분해 없이 행렬 M의 인수 분해를 수행합니다.

<region id="ID0EFQ2EB" actualWidth="478.01333333333338" actualHeight="62.800000000000004" top="2457.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="114">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m01</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

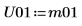
11. M = conj(U01T) x U01임을 보여줍니다.

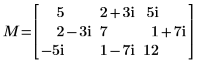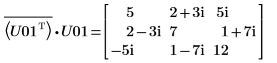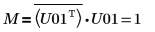관계는 논리적으로 참입니다.