예제: 식 인수 분해 및 전개
factor 키워드를 사용하여 정수, 라디칼 식 또는 대수 식을 인수 분해합니다.
expand 키워드를 사용하여 식을 전개합니다.
정수 인수 분해
1. 정수를 정의합니다.
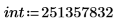
2. 기호 연산 연산자를 삽입합니다.
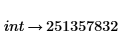
3. 기호 연산 연산자 위에 있는 자리 표시자에 factor 키워드를 입력한 다음 Enter 키를 누릅니다.
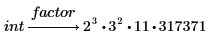
라디칼 식 인수 분해
1. 라디칼 식을 정의합니다.
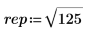
2. 기호 연산 연산자를 삽입합니다.
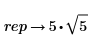
3. 기호 연산 연산자 위에 있는 자리 표시자에 factor 키워드를 입력한 다음 Enter 키를 누릅니다.
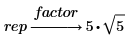
다항식 인수 분해
1. x의 다항식을 정의합니다.
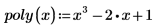
2. 기호 연산 연산자를 삽입합니다.
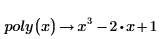
3. 기호 연산 연산자 위에 있는 자리 표시자에 factor 키워드를 입력한 다음 Enter 키를 누릅니다.
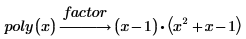
이 키워드는 유리수에 대해 다항식을 인수 분해합니다. 즉, 두 인수의 계수가 유리수(정수 또는 일반 분수)입니다. 두 번째 항은 더 이상 유리수로 인수 분해할 수 없습니다. 이것은 두 번째 항의 근이 무리수인 5의 제곱근을 포함하기 때문입니다.
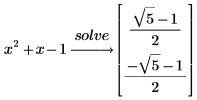
4. 벡터의 근을 구하는 solve 키워드를 사용하여 근을 구합니다.
5. 원래 다항식을 실수로 완전히 인수 분해하려면 factor 다음에 쉼표를 입력하고 쉼표 다음에 나타나는 자리 표시자에 5의 제곱근을 입력하여 5의 라디칼 식 제곱근을 인수로 추가합니다.
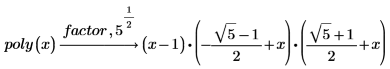
일반적으로 추가 인수 없이 factor 키워드를 사용하면 다항식이 다항식의 계수에서 생성된 수체로 인수 분해됩니다. 즉, 다항식의 계수가 모두 유리수이면 인수 분해의 계수가 모두 유리수여야 합니다. 하지만 다항식의 계수에 라디칼 식이 포함되어 있으면 인수 분해의 계수에도 동일한 라디칼 식이 포함될 수 있습니다. |
식 전개
1. expand 키워드를 사용하여 다음 식을 전개합니다.
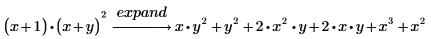
2. expand 다음에 쉼표를 입력한 다음 기본 식의 하위 식을 입력합니다.
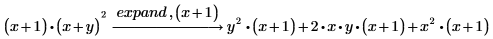
PTC Mathcad에서는 하위 식을 제외한 모든 항이 전개됩니다.
3. 원래 식에 없는 하위 식을 입력합니다.
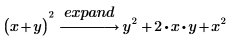
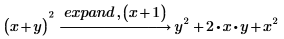
수정자를 포함하지 않은 경우와 결과가 동일합니다.
다항식을 실수에 대해 완전히 인수 분해
1. solve 키워드를 사용하여 실수에 대해 이 다항식의 실수 계수를 구합니다.
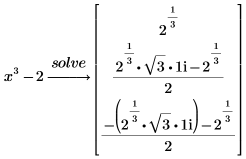
2. solve 키워드를 factor로 대체하고 다항식의 근에 나타나는 모든 라디칼의 목록을 쉼표로 구분하여 입력합니다.
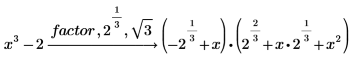
다항식을 복소수에 대해 완전히 인수 분해
1. 다항식을 복소수에 대해 완전히 인수 분해하려면 라디칼 목록에 복소수 1i를 추가합니다.
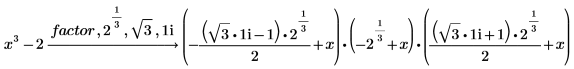
2. 또는 기호 근으로 벡터를 정의하고 factor 다음에 벡터 항목을 삽입합니다.
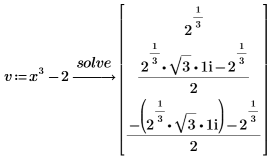
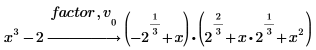
v0은 근에 나타나는 라디칼과 i를 모두 포함하므로 근 중 하나만 입력하면 됩니다.
3. real 또는 complex 수정자를 사용하여, 기호 계수가 아닌 부동소수점 계수로 실수 또는 복소수에 대해 다항식을 인수 분해합니다.

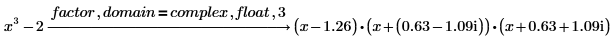
float 키워드는 계수에 표시되는 소수점 자릿수를 줄이는 데 사용됩니다.