예제: 고유 벡터 및 고유값
eigenvals, eigenvecs 및 eigenvec 함수를 사용하여 실수 또는 복소수 행렬의 고유값과 고유 벡터를 구합니다. 그리고 다음과 같은 숫자 λ를 구할 수 있는 경우 M이 정방 행렬이면 0이 아닌 벡터 v가 M의 고유 벡터라는 가설을 확인합니다.
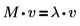
1. 입력 정방 행렬을 정의합니다.
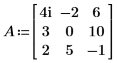
2. eigenvals 및 eigenvecs를 호출하여 행렬 A의 고유값과 고유 벡터를 구합니다.
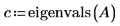
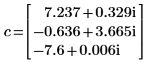
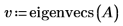

v의 첫 번째 열은 c의 첫 번째 요소에 해당하는 고유 벡터입니다. 마찬가지로, v의 두 번째 열은 c의 두 번째 요소에 해당하는 고유 벡터이며 이런 식으로 계속됩니다.
3. v1이 첫 번째 고유 벡터가 되도록 정의하고 c1이 A의 첫 번째 고유값이 되도록 정의합니다. A x v1과 c1 x v1을 비교합니다.
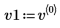
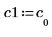
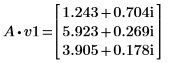 | 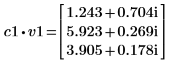 |
4. v2가 첫 번째 고유 벡터가 되도록 정의하고 c2가 A의 첫 번째 고유값이 되도록 정의합니다. A x v2와 c2 x v2를 비교합니다.
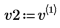
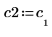
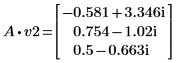 | 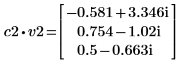 |
5. v3가 첫 번째 고유 벡터가 되도록 정의하고 c3가 A의 첫 번째 고유값이 되도록 정의합니다. A x v3와 c3 x v3를 비교합니다.
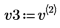
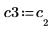
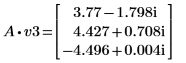 | 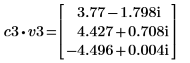 |
6. eigenvec 함수를 호출하여 특정 고유값에 대한 단일 고유 벡터를 구합니다.
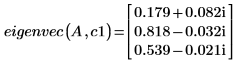

eigenvec 및 eigenvecs에서 구하는 결과가 반드시 일치해야 하는 것은 아니며 둘 모두 유효한 해입니다. 고유 벡터는 고유하지 않고, 배율 계수로 다른 고유 벡터와 연관됩니다. 그러므로 지정한 고유값에 대한 고유 벡터는 무한하게 많습니다.