예제: 이산 코사인 변환

함수 > 이미지 처리 > 변환 영역 > 예제: 이산 코사인 변환

예제: 이산 코사인 변환

dct 및 idct 함수를 사용하여 이산 코사인 변환 및 역 변환을 계산합니다. 이 변환의 이점은 이미지의 "에너지"(또는 정보)를 소수의 주파수 컴포넌트로 집중시켜 인코딩에 적합하게 만든다는 것입니다.

이 예제를 사용하는 것에 대한 자세한 내용은 이미지 처리 예제 정보를 참조하십시오.

1. 크기 N x P인 행렬 M을 정의합니다.

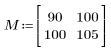
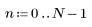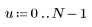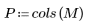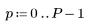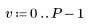2. 코사인 변환의 구현에서는 유형 II DCT(이산 코사인 변환)를 사용합니다. DCT를 이 변환의 분석식으로 정의합니다.

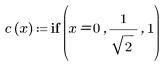
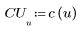
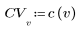
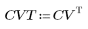
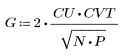
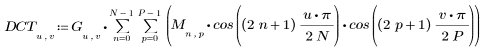
3. 행렬 DCT를 계산합니다.

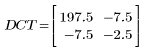
4. 함수 dct를 행렬 M에 적용합니다.

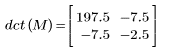
5. DCT 및 dct 함수 간의 최대 오차를 계산합니다.

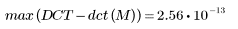
에너지 집중

코사인 변환은 뛰어난 에너지 집중 특성을 가지고 있습니다. 즉, 변환의 초반부의 계수 몇 개에 대부분의 에너지를 집중시킵니다.

1. 입력 행렬을 정의합니다.

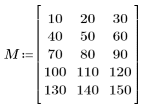
2. dct 함수를 행렬 M에 적용하고 계산합니다.

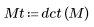
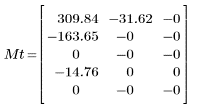
결과 행렬은 계수 값과 관련된 대부분의 에너지가 초반부의 요소 몇 개에 집중된다는 것을 보여줍니다.

idct

역 함수는 변환에서 원래 이미지를 복구하는 데 사용됩니다.

1. 모나리자의 흑백 버전을 읽습니다.

(mona.bmp)

2. dct 함수를 적용하여 이미지를 변환합니다.

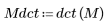
(mona_noise.bmp)

3. 역 함수를 적용하여 이미지를 복구합니다.

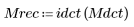
(mona_rec.bmp)

4. 변환 이미지와 원래 이미지의 히스토그램을 표시하여 DCT의 에너지 집중 특성을 확인합니다.

<region id="ID0EE43Y" top="3000" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">H</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">Horig</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

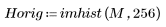
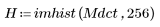
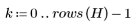
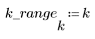
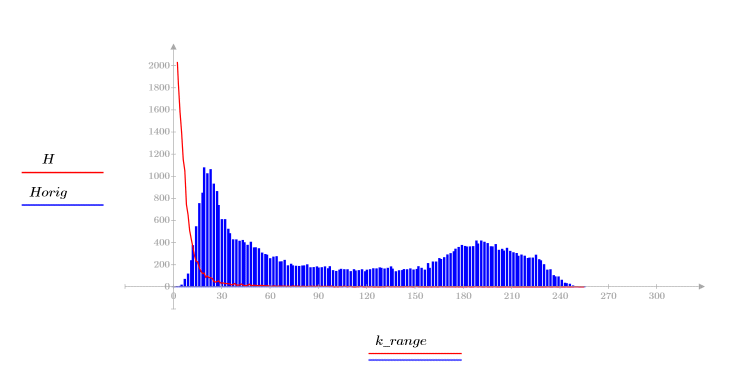
변환 이미지에서는 대부분의 에너지가 히스토그램의 초반부 빈 몇 개에 집중되어 있지만 원래 이미지에서는 넓게 분산되어 있습니다. 따라서 극소수의 주파수 컴포넌트로 대부분의 이미지 정보를 전달할 수 있는 변환 이미지가 인코딩이나 전송에 훨씬 적합합니다. 이러한 이유 때문에 이미지 압축에 DCT가 사용됩니다.