도함수 및 프라임 연산자
|
연산자
|
설명
|
키보드 단축키
|
|---|---|---|
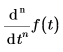 |
t를 기준으로 하여 점 t에서 계산한 f(t)의 n차 도함수를 구합니다.
• 숫자 연산의 경우 n은 0에서 5 사이의 자연수입니다.
• 기호 연산의 경우 n은 임의의 자연수입니다.
|
Ctrl+Shift+D
|
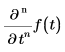 |
t를 기준으로 하여 점 t에서 계산한 f(t)의 n차 편도함수를 구합니다.
• 숫자 연산의 경우 n은 0에서 5 사이의 자연수입니다.
• 기호 연산의 경우 n은 임의의 자연수입니다.
|
Ctrl+D
|
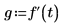 |
함수 g를 함수 f(t)의 1차 도함수로 정의합니다.
• n개의 프라임 연산자를 중첩시켜 nth(n차) 도함수를 구할 수 있습니다.
• 수치 연산이나 기호 연산에서 사용할 수 있는 프라임 연산자 수에는 제한이 없지만, 기호 연산의 계산 시간이 훨씬 빠릅니다.
|
Ctrl+'(아포스트로피)
|
피연산자
• f(t)는 스칼라 값 함수이며, 복소수가 사용될 수 있습니다.
◦ 도함수 연산자의 경우 f(t) 함수를 구성하는 변수의 개수에 제한이 없습니다.
◦ 프라임 연산자의 경우에는 f(t) 함수가 변수 하나로만 구성되어야 합니다.
• g는 함수 이름입니다.
• t는 도함수가 계산되는 점입니다.
추가 정보
• 식의 1차 도함수를 계산할 때에는 도함수 연산자의 지수 자리 표시자를 비워 둘 수 있습니다.
• 도함수를 계산한 값이 함수의 특이점에 너무 가깝지 않은 경우 1차 도함수는 유효 자릿수 7자리 또는 8자리 내에서 정확한 결과를 구할 수 있습니다. 도함수의 차수가 증가할 때마다 유효 자릿수의 약 한 자리만큼 정확도가 감소합니다.
• 도함수를 계산하는 데는 리더(Ridder) 방법을 변형한 수치 해석 방법이 사용됩니다. 이는 다양한 단계 크기를 사용하여 (n + 1) 점 분할 차분을 계산하는 방법입니다. 여기서 n은 도함수의 차수입니다. 그런 다음 가중평균을 사용하여 표의 연속 근사를 계산합니다. 연속되는 표 항목을 비교하고 오차가 허용되는 수준보다 작은 경우 오차가 가장 작은 항목을 도함수로 구합니다.