タスク 3-1: 状態空間での ODE のモデリング
以下に定義されている問題を読み、タスク 3 - 1 から 3 - 3 で、次の方法を使用して解を求めます。
• 状態空間 ODE ソルバ
• ODE ソルバ
• ソルブブロック
問題定義
古典的な質量-ばね-ダンパー系について考えます。
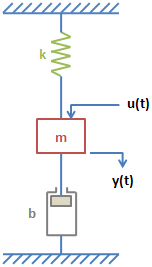
この系の運動方程式が次の式によって与えられます。
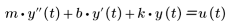
この系を次の形式の状態空間モデルによって表すことができます。
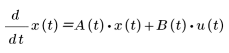
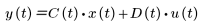
ここで
• A - 状態行列
• B - 入力行列
• C - 出力行列
• D - 直達行列
• x - 状態ベクトル
• u - 入力
• y - 測定/被制御出力
系の運動をモデル化する状態と出力の非線形方程式を線形化することで、上記の線形系を求めることができます。 |
この 2 次系では 2 つの状態変数を使用します。
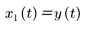
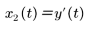
m = 1、b = 0.5、k = 3 とした場合、系の方程式は次のようになります。
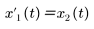
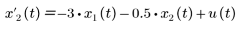
状態空間行列の形式では、モデルは次のように表されます。
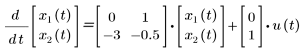
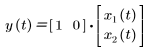
状態空間 ODE ソルバ
1. 行列関数 A、B、C、および D を定義します。
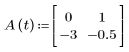 | 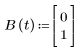 |
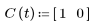 | 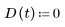 |
2. 入力をヘビサイドのステップ関数として定義します。このステップ関数を挿入するため、F と入力してから Ctrl + G キーを押します。
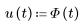
3. 2 つの変数の初期条件を定義します。i をリテラル下付き文字として入力するため、「数式」タブの「スタイル」グループで、「下付き文字」をクリックし、i と入力します。
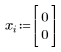
4. 系の解を求める時間境界を定義します。
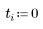
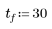
5. 解を求める ti 以外の点の数を定義します。
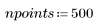
6. statespace 関数を呼び出します。
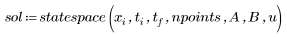
行列 sol の最初の列には、解を求めた時間が格納されています。この行列のその他の列には、その時間における状態変数 x1 と x2 の値が格納されています。
7. 行列 sol から t、x1、x2 を抽出します。
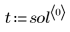 | 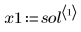 | 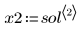 |
 |  |  |
8. x1 の平均値と最大値を計算します。
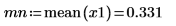
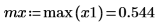
9. 時間に対して x1 をプロットし、マーカーを使用して平均値と最大値を表示します。
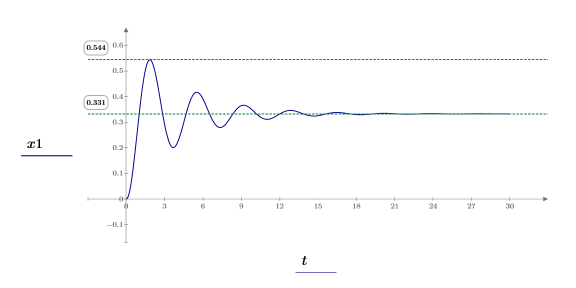
プロットには、立上がり時間、オーバーシュート、整定時間などの過渡応答特性が示されます。