Fonctions gamma symboliques
• Psi(z) : renvoie la dérivée du logarithme naturel de la fonction gamma Γ(z). La fonction digamma est définie comme suit :
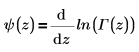
• Psi(n, z) : renvoie la nth dérivée de Psi(z). La fonction polygamma est définie comme suit :
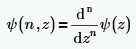
Psi(z) se rapporte à Psi(n, z) comme suit :
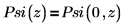
Arguments
• z est un scalaire réel ou complexe, ou un vecteur de scalaires réels ou complexes.
• n est un entier non négatif.
Informations supplémentaires
• Vous pouvez évaluer la version à un seul argument de la fonction Psi à la fois de manière symbolique et numérique. Si vous l'évaluez de manière numérique, z peut également être un scalaire complexe ou un vecteur de scalaires complexes.
• Vous ne pouvez évaluer la version à deux arguments de la Psi fonction que de manière symbolique.