Exemple : Utilisation des unités avec les fonctions d'interpolation polynomiale

Fonctions > Analyse des données > Interpolation et prévision > Exemple : Utilisation des unités avec les fonctions d'interpolation polynomiale

1. Définissez deux vecteurs d'entrée et une variable indépendante.

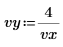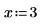2. Définissez les unités.

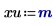
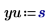
3. Evaluez les vecteurs d'entrée et la variable d'entrée.

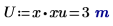L'unité de la variable indépendante U doit correspondre à l'unité du vecteur du premier argument.

Interpolation polynomiale

1. Utilisez la fonction polyint pour évaluer la fonction d'interpolation aux valeurs de variables indépendantes spécifiées.

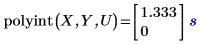
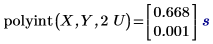
Le fait de rechercher U dans le vecteur d'entrée X engendre une correspondance. La valeur exacte correspondante dans le vecteur Y est 1.333 avec une erreur de zéro. Cependant, 2U n'a aucune correspondance exacte dans X et cela engendre une valeur interpolée avec une erreur différente de zéro.

2. Utilisez la fonction length pour déterminer la longueur des vecteurs d'entrée, puis créez un programme court pour évaluer les fonctions d'interpolation à différents points. Affichez les points interpolés dans la première colonne et les valeurs d'erreur dans la seconde.

<region id="ID0EJKCU" actualWidth="485.86333333333334" actualHeight="197.304" top="1075.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="45">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <eval>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L</id>
 </range>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>1</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </program>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

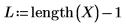
La variable u doit être un scalaire, et l'unité m est ajoutée comme partie de l'argument de fonction.

3. Enregistrez les points d'interpolation et les valeurs d'erreur sous forme de deux vecteurs séparés.

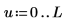
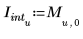
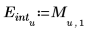
4. Tracez les points d'interpolation avec l'enveloppe d'erreur.

<region id="ID0ESOCU" actualWidth="576" actualHeight="307.2" top="1401.6000000000001" left="38.400000000000006" height="307.2" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="49">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="50">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lignes</traceStyle>
 </trace>
 <trace resultRef="51">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="418.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="52">
 <real xmlns="http://schemas.mathsoft.com/math50">0.9</real>
 </secondTickValue>
 <endValue resultRef="53">
 <real xmlns="http://schemas.mathsoft.com/math50">9</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="126.556666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

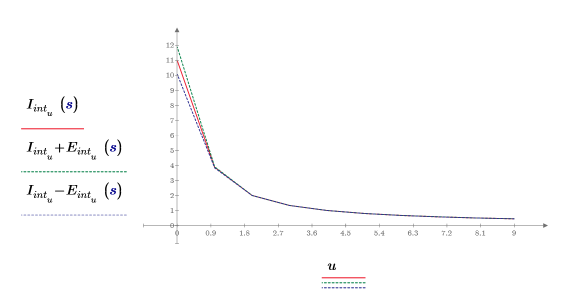
L'erreur est relativement grande au début puis devient négligeable après le second point d'interpolation.

Itération polynomiale

1. Utilisez la fonction polyiter pour évaluer la fonction d'itération à la valeur de variable indépendante spécifiée, le nombre maximal d'itérations et la tolérance.

<region id="ID0EXQCU" actualWidth="261.85" actualHeight="62.800000000000004" top="1900.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="54">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>2</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0EFRCU" actualWidth="261.85" actualHeight="62.800000000000004" top="1977.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="55">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>5</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

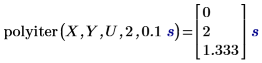
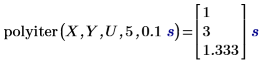
• L'algorithme s'arrête si les deux estimations d'itération du point de données sont équivalentes à l'intérieur de la valeur de tolérance , ou si le nombre d'itérations atteint le nombre maximal autorisé d'itérations.

• Le premier résultat indique que la fonction d'itération n'a pas pu converger après avoir atteint le nombre maximal autorisé de deux itérations. Il a donc renvoyé l'élément correspondant dans le vecteur Y.

• Le second résultat indique que la fonction d'itération a convergé après la troisième itération et qu'elle n'a pas atteint le nombre maximal autorisé de cinq itérations.

2. Utilisez un programme court pour évaluer la fonction d'itération à dix points différents. Utilisez l'augment de fonction pour ajouter la valeur d'erreur dans la quatrième colonne de la matrice renvoyée qui affiche le statut de fusion dans la première colonne, le nombre d'itérations utilisées dans la seconde, et les valeurs itérées dans la troisième.

<region id="ID0EZWCU" actualWidth="487.13666666666654" actualHeight="200.2" top="2284.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="56">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">
 P<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">ord</id>
 <id labels="VARIABLE" xml:space="preserve">err</id>
 </boundVars>
 </function>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">order</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ord</id>
 </localDefine>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">error</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">err</id>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <apply>
 <minus />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">length</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 </apply>
 <real>1</real>
 </apply>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">K</id>
 <id labels="*" xml:space="preserve">u</id>
 </apply>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>2</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">N</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">order</id>
 <apply>
 <scale />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve">s</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">Z</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">augment</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 </sequence>
 </apply>
 </localDefine>
 <return>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Z</id>
 </return>
 </program>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

3. Enregistrez les points d'interpolation et les valeurs d'erreur sous forme de vecteurs séparés.

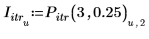
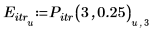
4. Tracez les points d'itérations pour 3 itérations et une erreur de 0.25.

<region id="ID0EH1CU" actualWidth="577" actualHeight="307.20000000000005" top="2707.2000000000003" left="38.400000000000006" height="307.20000000000005" width="577" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="59">
 <traceStyle color="#FFED1D2F" symbol="filledRectangle" line-weight="1" line-style="Solid">lignes</traceStyle>
 </trace>
 <trace resultRef="60">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Dash">lignes</traceStyle>
 </trace>
 <trace resultRef="61">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="419.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="bottom" positionticmark="-1" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>10</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="62">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0.25" end="3.55">
 <axisLine position="origin" positionticmark="0" legendWidth="123.37" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

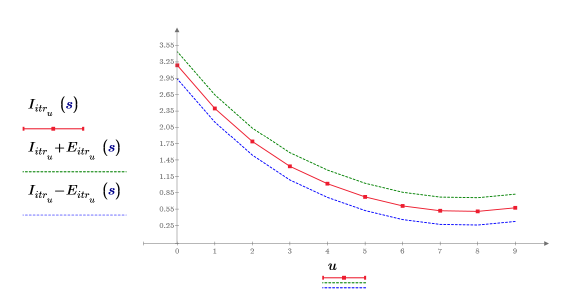
L'erreur est constante à tous les points d'interpolation.

5. Comparez les résultats d'interpolation et d'itération renvoyés lorsque le nombre maximal d'itérations est défini sur 3 et que l'erreur est définie sur 0.25.

<region id="ID0E22CU" actualWidth="576.60000000000014" actualHeight="287.99999999999994" top="3129.6000000000004" left="38.400000000000006" height="287.99999999999994" width="576.60000000000014" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="63">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lignes</traceStyle>
 </trace>
 <trace resultRef="64">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="81.1466666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

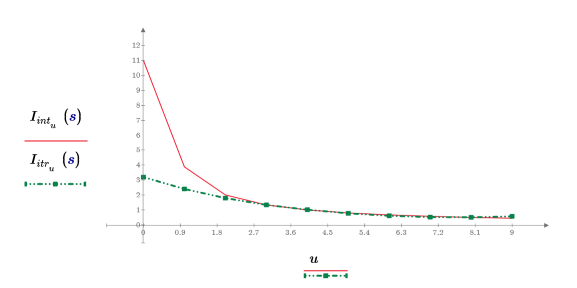
6. Montrez que le résultat d'interpolation est identique au résultat d'itération lorsque le nombre d'itérations est défini sur un nombre important et que l'erreur est définie sur zéro.

<region id="ID0EZ4CU" actualWidth="576.6" actualHeight="288" top="3571.2000000000007" left="38.400000000000006" height="288" width="576.6" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="66">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="67">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="87.5333333333333" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I0<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

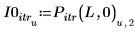
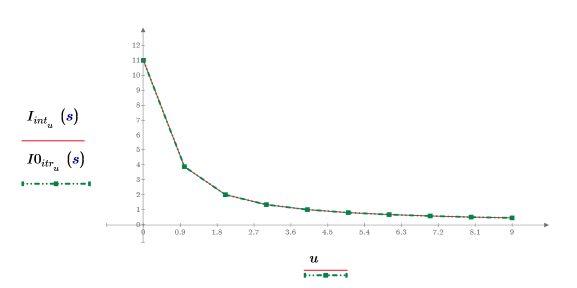
Le nombre maximal d'itérations doit être inférieur à la longueur des vecteurs d'entrée.

Rubriques associées

Interpolation polynomiale

Est-ce que cela a été utile ?