Exemple : Utilisation de l'opérateur de limites
Utilisation de l'infini comme valeur limite
1. Utilisez l'opérateur de limites et évaluez de manière symbolique une expression lorsque son argument approche l'infini.
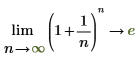
2. Tracez la fonction pour faciliter sa visualisation. Utilisez un marqueur horizontal pour représenter e.
 |  |  |
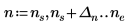 | ||
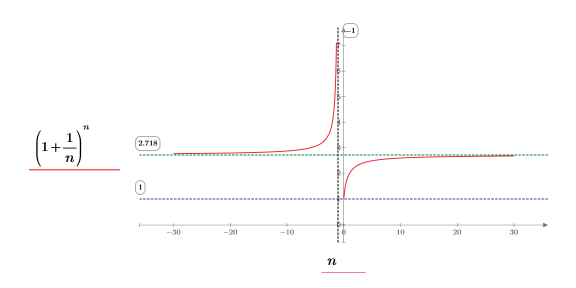 | ||
Dans le quadrant (x, y) nous observons les éléments suivants :
◦ Lorsque n approche positive infinity, la fonction approche y=e.
◦ Lorsque n approche 0, la fonction approche y=1.
Mathématiquement, ceci est représenté par les évaluations symboliques suivantes :
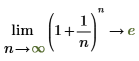 | 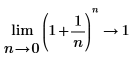 |
Dans le quadrant (-x, y) nous observons les éléments suivants :
◦ Lorsque n approche negative infinity, la fonction approche y=e.
◦ Lorsque n approche -1, la fonction approche y=infinity.
Mathématiquement, ceci est représenté par les évaluations symboliques suivantes :
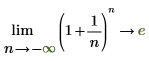 | 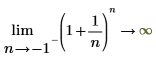 |
L'utilisation de limite à gauche dans la deuxième équation implique que la -1 doit être approchée à partir de la partie gauche de la courbe. Si ce n'est pas spécifié, l'évaluation renvoie "undefined", car la fonction n'est pas définie pour -1 < n < 0 : 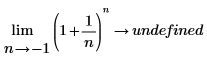 |
Utilisation du côté de la limite
1. Tracez la fonction cot.
 | 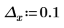 | 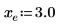 |
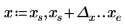 | ||
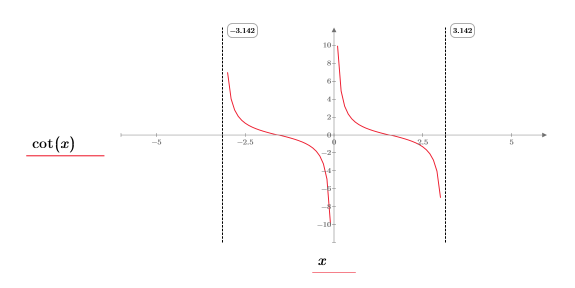 | ||
Dans le quadrant (x, y) nous observons les éléments suivants :
◦ Lorsque x approche 0, la fonction approche y=infinity.
◦ Lorsque x approche π, la fonction approche y=-infinity.
Mathématiquement, ceci est représenté par les évaluations symboliques suivantes :
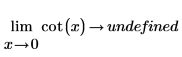 | 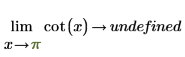 |
Dans la mesure où la fonction est symétrique autour de x=+/- n*π/2, l'évaluation symbolique renvoie "undefined", car la fonction autour de x=0 (et tout multiple de π) peut être infinity ou -infinity, en fonction du côté à partir duquel x approche 0.
Il s'agit d'un cas intéressant pour spécifier le "côté limite".
2. Spécifiez le "côté limite" et réévaluez de façon symbolique la fonction cot autour de 0 et de π.
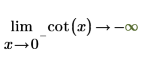 | 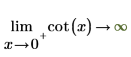 |
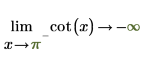 | 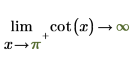 |
Les résultats renvoyés concordent avec le tracé.
Parfois, il peut être utile de tracer une fonction afin de la visualiser et de vérifier la validité des résultats de l'évaluation symbolique. |