Fonctions > Traitement du signal > Transformées supplémentaires > Exemple : Transformée de Hartley
Exemple : Transformée de Hartley
Utilisez la fonction dht pour rechercher la transformée de Hartley des signaux.
La somme de définition de la transformée de Hartley est analogue à la somme de la transformée de Fourier discrète.
Cliquez pour copier cette expression
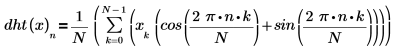
où N correspond au nombre d'éléments dans le tableau de données réelles x.
Somme de courbes sinusoïdales
Recherchez la transformée de Hartley pour une somme de courbes sinusoïdales et comparez-la à l'amplitude de la transformée complexe de Fourier.
1. Définissez le nombre d'éléments.
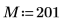
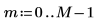
Cliquez pour copier cette expression
Cliquez pour copier cette expression
2. Utilisez la fonction sin pour définir le signal d'entrée.
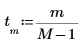
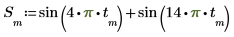
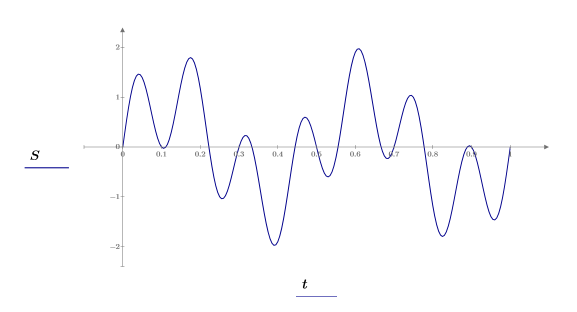
Cliquez pour copier cette expression
Cliquez pour copier cette expression
3. Tracez le signal.
Cliquez pour copier cette expression
4. Utilisez la fonction dht pour afficher les fréquences discrètes représentées dans les deux courbes sinusoïdales, puis utilisez la fonction center pour déplacer le composant DC vers le centre.
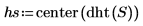
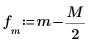
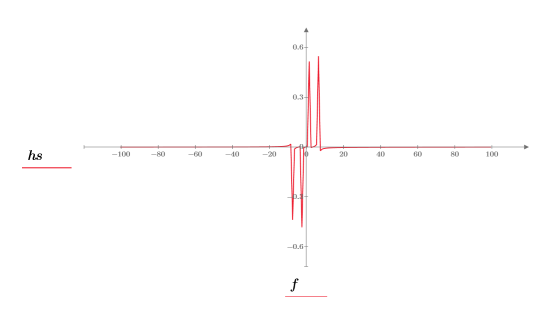
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
5. Utilisez les fonctions match et max pour trouver les fréquences discrètes auxquelles les pics se produisent et marquez un de ces points avec un marqueur vertical et horizontal.
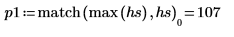
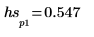
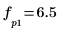
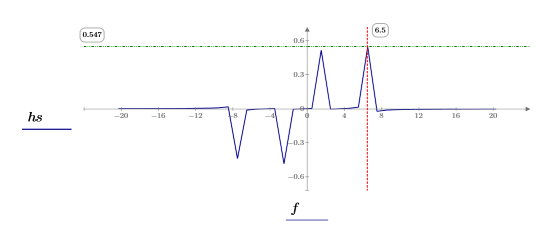
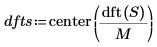
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
6. Utilisez les fonctions dft et center pour obtenir et centrer la transformée de Fourier discrète.
Cliquez pour copier cette expression
7. Tracez les valeurs absolues du DFT.
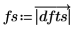
Cliquez pour copier cette expression
Cliquez pour copier cette expression
8. Utilisez les fonctions match et max pour trouver les fréquences discrètes auxquelles les pics se produisent.
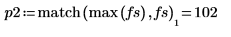
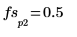
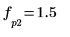
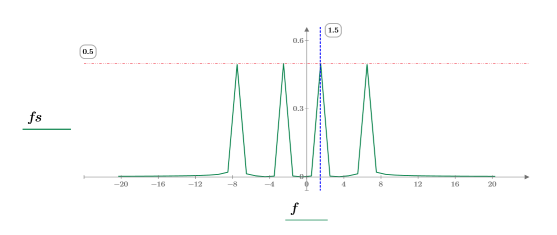
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation étroite entre la transformée de Hartley et la transformée de Fourier peut être démontrée en montrant comment calculer la phase et l'amplitude grâce à la transformée de Fourier. Ceci peut être réalisé à l'aide d'un petit jeu de données.
Signal court et bruyant
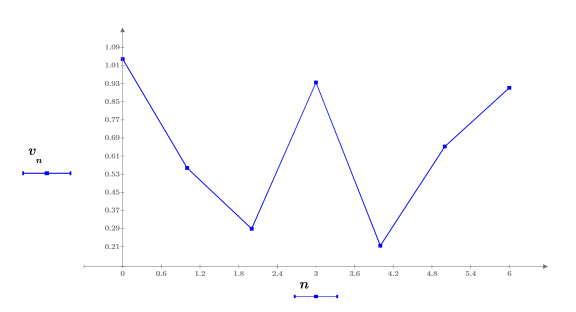
1. Définissez et tracez un signal d'entrée parasité de 7 points d'échantillonnage.
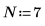
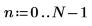
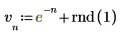
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
2. Calculez et centrez la transformée de Hartley discrète.
Cliquez pour copier cette expression
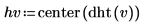
3. Calculez les parties paires et impaires de la transformée de Hartley discrète (ces formules partent d'une valeur impaire de N).
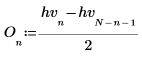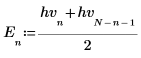Cliquez pour copier cette expression
Cliquez pour copier cette expression
4. Utilisez la fonction angle pour calculer le vecteur de phase.
Cliquez pour copier cette expression
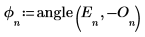
5. Définissez le vecteur d'amplitude.
Cliquez pour copier cette expression
6. Utilisez les fonctions phase, phasecor et center pour créer le vecteur de phase.
Cliquez pour copier cette expression
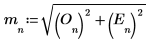
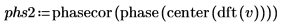
7. Utilisez la fonction augment pour comparer les résultats de phase à ceux obtenus grâce à la transformée de Fourier.
Cliquez pour copier cette expression
Les résultats de phase sont concordants.
8. Utilisez les fonctions dft et center pour créer le vecteur d'amplitude.
Cliquez pour copier cette expression
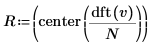
9. Utilisez la fonction augment pour comparer les résultats d'amplitude à ceux obtenus grâce à la transformée de Fourier.
Cliquez pour copier cette expression
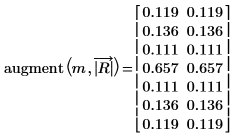
Les résultats d'amplitude sont concordants.
Pour obtenir des explications détaillées sur la transformée de Hartley et ses applications, consultez l'ouvrage de Ronald Bracewell, The Hartley Transform (Oxford University Press).
Transformée de Hartley
Pour ajouter, déplacer ou supprimer un marqueur
Est-ce que cela a été utile ?