Fonctions > Traitement du signal > Analyse spectrale > Exemple : La transformée en z chirp
Exemple : La transformée en z chirp
La transformée en z chirp utilise le spectre d'un signal échantillonné et interpole les valeurs à des fréquences uniformément espacées sur un intervalle de fréquences réduit.
L'algorithme utilisé est la transformée en z chirp décrite par Samuel Stearns et Ruth David, dans Signal Processing Algorithms (Prentice-Hall, Inc.).
Création du signal
1. Définissez les fréquences du signal.
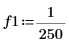
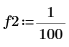
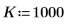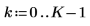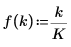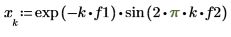Cliquez pour copier cette expression
Cliquez pour copier cette expression
2. Utilisez les fonctions exp et sin pour définir un signal d'onde sinusoïdale décroissant.
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Le signal d'onde sinusoïdale décroissant est le produit d'une fonction exponentielle qui décroît vers zéro dans le temps et une fonction d'onde sinusoïdale.
3. Tracez le signal décroissant.
Cliquez pour copier cette expression
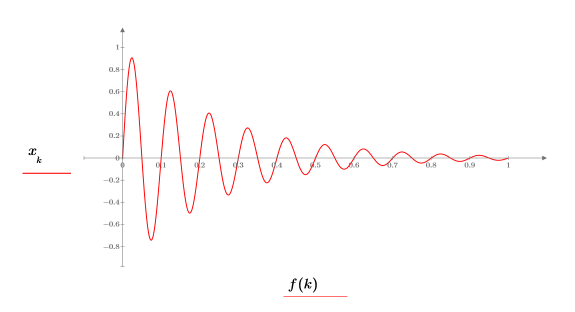
La fréquence est normalisée, de sorte que 1 représente la fréquence d'échantillonnage.
4. Utilisez la fonction dft pour calculer la DFT du signal.
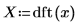
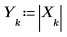
Cliquez pour copier cette expression
Cliquez pour copier cette expression
5. Tracez la DFT du signal. Utilisez les marqueurs verticaux pour afficher l'amplitude et la fréquence du premier pic.
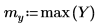
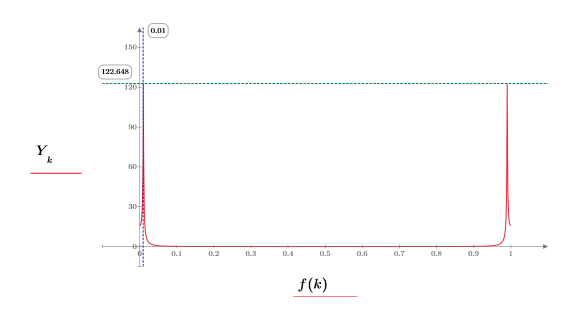
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Le pic se produit à la fréquence de l'onde sinusoïdale, convoluée avec le spectre de l'exponentielle.
6. Zoomez sur le premier pic en développant l'échelle de fréquence sur l'axe x.
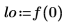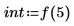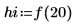Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
7. Calculez le nombre de points de données dans la plage de fréquences.
Cliquez pour copier cette expression
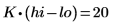
chirpz
Utilisez la fonction chirpz pour obtenir un spectre autour du pic plus approfondi en augmentant le nombre de points de données.
1. Définissez le paramètre d'incrément et utilisez la fonction chirpz pour calculer le spectre.
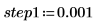
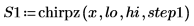
Cliquez pour copier cette expression
Cliquez pour copier cette expression
2. Calculez le nombre de points dans le spectre interpolé.
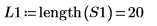
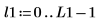
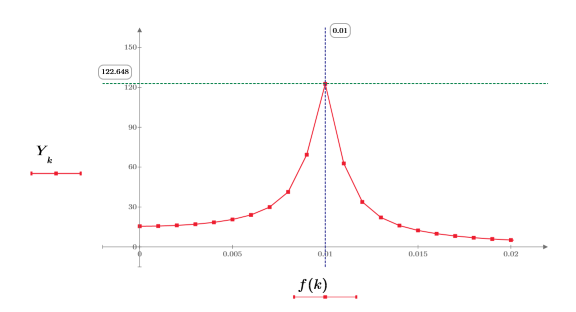
Cliquez pour copier cette expression
Cliquez pour copier cette expression
3. Surimposez le premier pic de la DFT et le spectre interpolé à l'aide de la nouvelle plage.
Cliquez pour copier cette expression
Un incrément de 0.001 génère le même nombre de points de données dans la trace chirp-z et par conséquent, les deux courbes apparaissent identiques.
4. Réduisez de 10 la taille des incréments, puis recalculez et retracez les deux fonctions.
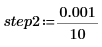
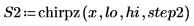
Cliquez pour copier cette expression
Cliquez pour copier cette expression
5. Calculez le nouveau nombre de points dans le spectre interpolé.
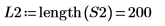
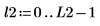
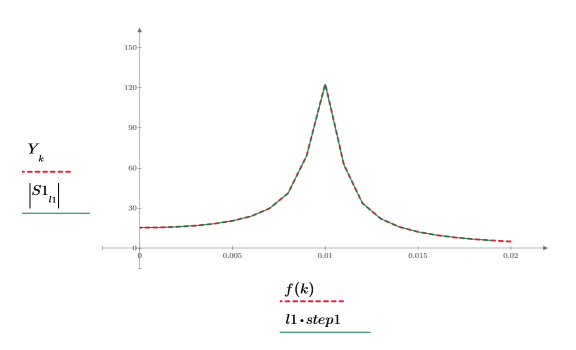
Cliquez pour copier cette expression
Cliquez pour copier cette expression
6. Surimposez le premier pic de la DFT et nouveau spectre interpolé.
Cliquez pour copier cette expression
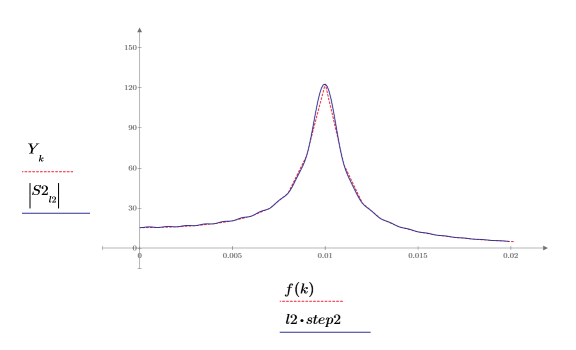
Le tracé indique que lorsque le nombre de points interpolés augmente, la courbe du spectre s'arrondit autour du pic.
7. Réduisez encore 10 fois step2 et observez les effets sur le tracé ci-dessus.
Transformée en z chirp
Est-ce que cela a été utile ?