Fonctions logarithmiques et exponentielles
• exp(z) : renvoie le nombre e élevé à la puissance z.
• log(z, [b]) : renvoie le logarithme de base b de z. Si b est omis, renvoie le logarithme de base de 10 de z.
• ln(z) : renvoie le logarithme naturel (base e) de z.
• ln0(z) : renvoie le logarithme naturel (base e) de z, mais renvoie –1×10307 à z = 0.
Arguments
• z est un scalaire sans dimension (réel, complexe ou imaginaire) ou un vecteur de scalaires.
Pour les fonctions log et ln, z ne peut pas être zéro. Si z est un vecteur, alors aucun de ses éléments ne peut être zéro.
• b (facultatif) est un scalaire réel positif ou un vecteur scalaire. S'il est omis, b est supposé égal à 10.
Si b est un vecteur, alors aucun de ses éléments ne peut être zéro et il doit avoir la même longueur que le vecteur z.
|
|
• Si z est complexe, les fonctions log renvoient des valeurs provenant de la branche principale de ces fonctions, ou ln(z) = ln(|z|) + i arg(z)
• La fonction exp est équivalente à l'élévation de e à une puissance, mais les algorithmes utilisés sont différents. Pour des valeurs d'exposant très élevées ou très faibles, cet algorithme est plus fiable et évite les erreurs d'arrondis numériques. L'évaluation symbolique de exp(x) avec un argument décimal permet de trouver les valeurs les plus précises pour les très grands arguments : 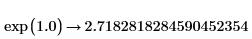 |