Exemple : Solutions symboliques d'équations
Résolvez des équations de manière symbolique dans une ou plusieurs inconnues.
Résolution d'une équation unique
1. Saisissez l'équation suivante :
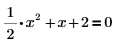
2. Insérez l'opérateur d'évaluation symbolique, saisissez le mot-clé solve dans la marque de réservation, puis appuyez sur Entrée.
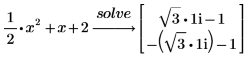
Le côté droit de l'équation étant égal à 0, il n'est pas nécessaire de saisir la partie =0 de l'expression. |
3. Saisissez la constante 2 au format décimal sous la forme 2.0 afin de renvoyer la réponse au format de virgule flottante.
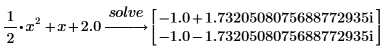
4. Résoudre une équation à une variable
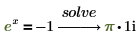
5. Résoudre une équation à plusieurs variables
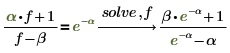
Lorsque l'équation comporte plusieurs variables, vous devez tout d'abord spécifier la variable à résoudre. |
6. Résoudre un polynôme d'ordre quatre.

Le résultat ci-dessus montre que la solution symbolique d'un polynôme d'ordre quatre produit quatre solutions numériques. |
7. Recherchez les racines d'un polynôme avec des coefficients paramétrés.
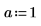
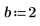
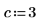
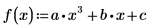
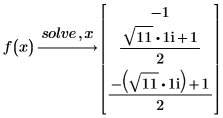
Résolution de systèmes d'Equations et d'égalités
Vous pouvez résoudre plusieurs équations et égalités ensemble en tant que système d'équation en les regroupant dans un vecteur.
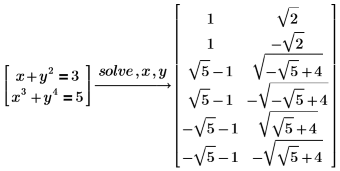
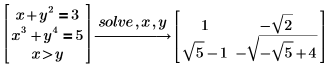
Résolution de polynômes dans des radicaux
Par défaut, PTC Mathcad résout les équations de polynômes jusqu'au degré 4 de radicaux. Les solutions sont intégrées, à l'aide d'opérations ordinaires d'arithmétique, en termes de radicaux.
1. Résolvez le polynôme suivant :
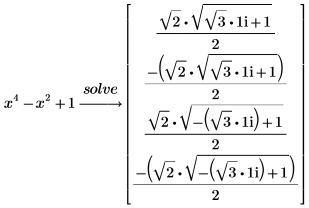
Le mathématicien Galois a démontré, au 19ème siècle, qu'il existe des polynômes de degré 5 et supérieur qui ne peuvent pas être résolus en termes de radicaux. Pour ces polynômes, PTC Mathcad renvoie une approximation numérique pour les racines. |
2. Résolvez un polynôme de degré 5.

Le résultat ci-dessus montre que la solution symbolique d'un polynôme d'ordre cinq produit cinq solutions numériques. |
Hypothèses sur le domaine d'une variable
Le mot-clé assume permet d'émettre des hypothèses sur le domaine d'une variable du problème, par exemple qu'il s'agit d'un nombre réel.
1. Résolvez une équation en supposant que x est un nombre réel :
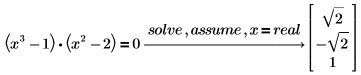
PTC Mathcad renvoie uniquement les solutions avec nombres réels à l'équation. |
2. Utilisez RealRange pour rechercher les solutions avec nombres réels dans la plage (0, 2).
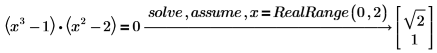
3. Saisissez x=integer pour rechercher uniquement les solutions avec nombres entiers.
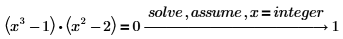
4. Utilisez assume pour limiter le domaine d'une variable dans une évaluation symbolique.
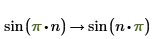
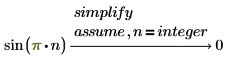
Renvoie de solutions détaillées aux équations
Ajoutez le modificateur fully après la résolution pour renvoyer des solutions détaillées aux équations.
1. Utilisez la fonction clear.sym pour effacer la valeur symbolique précédente de a :
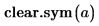
2. Utilisez fully pour renvoyer les valeurs de a pour lesquelles la solution est valide.
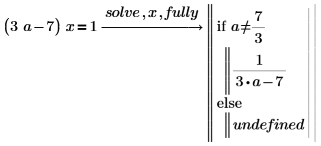
3. Le résultat détaillé permet de définir une fonction.
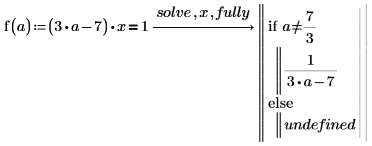
4. Evaluez la fonction pour a=3 et a=7/3 :
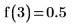
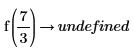
Equations avec solutions périodiques
Pour les équations dont la solution est périodique, PTC Mathcadrenvoie une solution unique, suivie d'une expression pour ajouter des multiples d'entiers de la période à la première solution.
1. Utilisez fully pour évaluer sin(x).
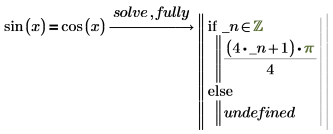
L'expression qui suit l'instruction if signifie pi/4 plus tous les multiples de type entier de pi. PTC Mathcad insère une variable _n nouvellement générée qui représente un entier arbitraire. Un trait de soulignement est inséré avant la variable générée afin d'éviter les conflits de nom avec d'autres variables qui peuvent être définies ailleurs dans le document. |
2. Ajoutez le modificateur using, suivi d'une équation écrite en utilisant l'opérateur booléen "égal à" pour définir la variable générée égale à la nouvelle variable.
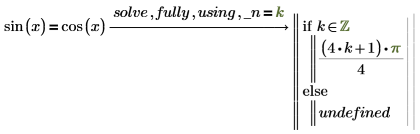
Si la variable que vous spécifiez après using n'est pas la variable générée que solve aurait renvoyée, PTC Mathcad renvoie une erreur.