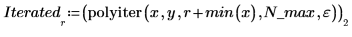Exemple : Interpolation polynomiale
polyint
Utilisez la fonction polyint pour réaliser une interpolation polynomiale sur un jeu de données.
1. Définissez un jeu de données.


2. Appelez la fonction polyint pour calculer l'interpolation polynomiale du jeu de données d'un point particulier.
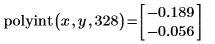
A x = 328, le résultat interpolé est y = -0.189, avec une erreur de 0.056.
3. Définissez la plage de valeurs x où vous voulez trouver les valeurs interpolées y.
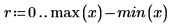
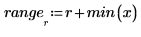
4. Enregistrez les valeurs interpolées et leur erreur respective.
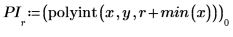
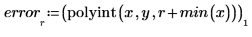
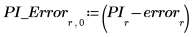
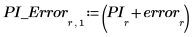
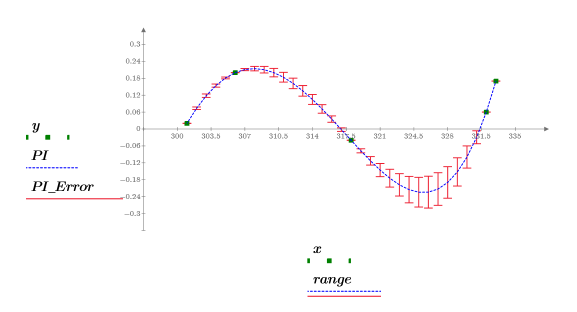
5. Tracez les points de données, la courbe interpolée et l'estimation d'erreur.
polycoeff
Pour calculer les valeurs interpolées, utilisez polyint. Pour calculer le polynôme d'interpolation et certaines de ses dérivées, utilisez polycoeff. Les coefficients fournis par polycoeff sont moins précis à des points données. Ils ne constituent donc pas la meilleure représentation des valeurs interpolées.
1. Trouvez les coefficients polynomiaux pour la courbe polynomiale qui traverse l'ensemble de points de données défini ci-dessus.
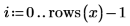
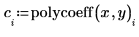
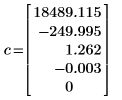
2. Définissez une fonction polynomiale, où c correspond au vecteur des coefficients polynomiaux.
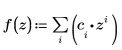
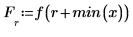
3. Différenciez la fonction polynomiale.
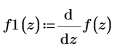
4. Tracez les points de données, l'interpolation polynomiale et sa dérivée première.
La fonction polycoeff n'élabore pas le polynôme du meilleur ajustement par la méthode des moindres carrés, qui est alors effectué par la fonction polyfit.
Les résultats de polyint et polycoeff ne doivent pas être utilisés pour réaliser des prévisions pour les valeurs y en dehors des valeurs x d'origine.
polyiter
Utilisez la fonction polyiter pour réaliser une interpolation polynomiale.
1. Définissez le nombre maximum possible d'itérations et la tolérance.
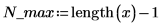
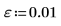
2. Appelez la fonction polyiter.
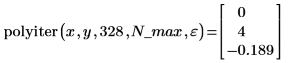
L'algorithme ne converge pas : il ne s'est donc pas arrêté avant l'itération N_max. Il n'a pas généré d'erreur de 0.01 et il a renvoyé le même résultat que polyint :
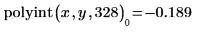
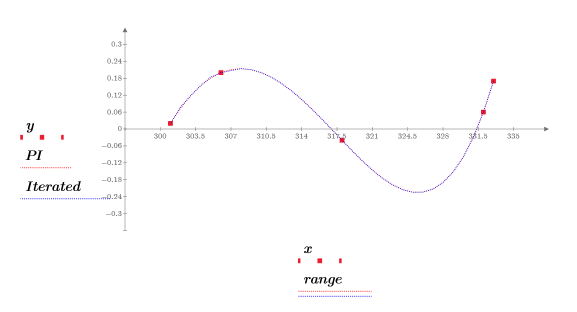
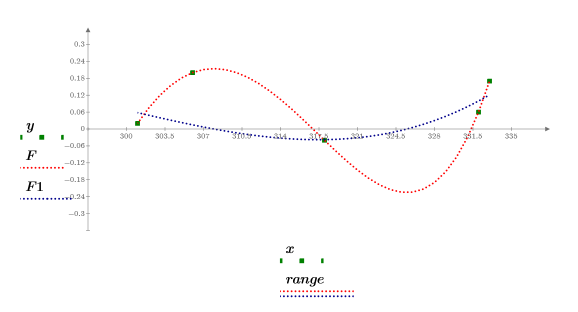
3. Tracez les points d'origine, le polynôme exact et le polynôme itéré.