Exemple : Générateurs de bruit
Utilisez les fonctions de whiten, gaussn et onefn pour simuler des bruits blancs, gaussiens et 1/f respectivement.
Bruit blanc
La fonction whiten simule le bruit généré par N sources indépendantes, chacune d'entre elles présentant une sortie aléatoire selon une distribution uniforme comprise entre -0.5 et 0.5.
1. Utilisez la fonction whiten pour évaluer la fonction de bruit blanc pour six sources de bruit indépendantes.

La répétition de l'évaluation de la fonction whiten génère un autre jeu de valeurs du vecteur.
2. Considérez un vecteur de sortie un peu plus grand.
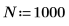
3. Tracez la fonction de bruit blanc.
4. Utilisez les fonctions mean et stdev pour calculer la moyenne et l'écart-type du vecteur de bruit blanc.
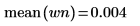
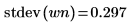
5. Affichez la valeur théorique de la moyenne, puis utilisez la fonction var pour calculer l'écart-type.
Le tracé montre que le signal wn a une moyenne théorique égale à 0. | |
L'écart-type est égal à la racine carrée de la variance. | 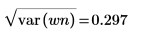 |
6. Comparez les valeurs calculées de la moyenne et de l'écart-type aux valeurs théoriques et vous verrez qu'elles n'en diffèrent pas de manière significative.
Bruit gaussien
La fonction gaussn simule un nombre x de sources de bruit indépendantes, chacune d'entre elles suivant une distribution de probabilité gaussienne de moyenne 0 et d'écart-type 1.
1. Evaluez la fonction de bruit gaussian pour six sources de bruit indépendantes.

Les éléments d'un vecteur peuvent en théorie avoir n'importe quelle valeur réelle, mais ils sont généralement compris entre -3 et +3. Vous pouvez le vérifier en appuyant sur F5 pour recalculer la fonction.
2. Tracez une séquence gaussienne de l'échantillon.
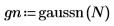
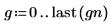
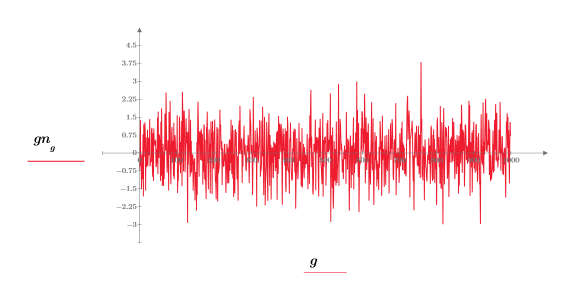
3. Préparez les données de Gauss pour un tracé de l'histogramme en cloche en regroupant les valeurs en 20 emplacements de 0,05 de large.
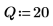
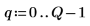
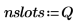
4. Définissez le vecteur qui contient les limites des emplacements et définissez la frontière la plus à droite.
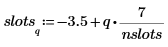
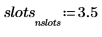
5. Utilisez la fonction hist pour créer l'histogramme et tracer un graphique à barres.
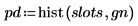
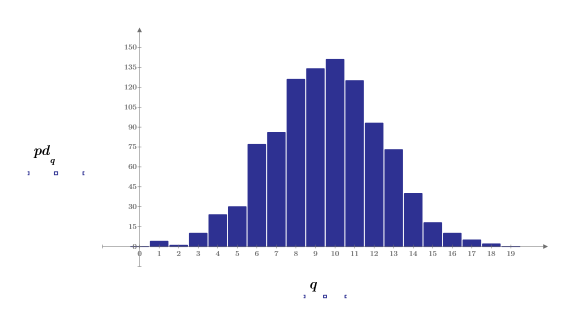
6. Comparez la moyenne et l'écart-type de l'échantillon aux valeurs prévues 0 et 1.
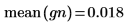
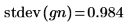
Bruit 1/f
La fonction onefn calcule une approximation du bruit 1/f à l'aide d'une routine basée sur un algorithme développé par Richard Voss (voir l'article de Martin Gardner dans la revue Scientific American d'avril 1978).
1. Utilisez la fonction onefn permettant de générer un vecteur 1/f de 1 000 points.
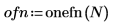
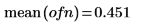
2. Ajustez à la moyenne 0.
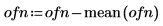
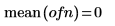
3. Tracez les données de vecteur.
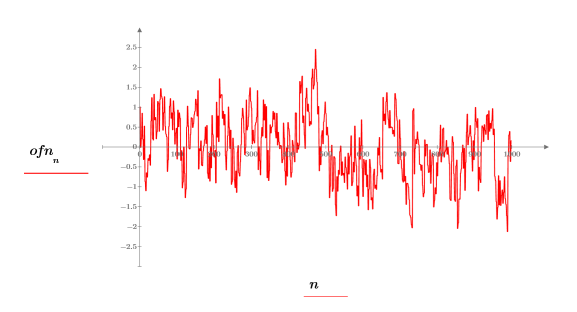
On trouve des bruits 1/f dans les signaux de nombreux phénomènes naturels ou de phénomènes créés par l'homme, comme la musique, les signaux émis par le cerveau, les conditions atmosphériques, les mouvements sur le marché des actions et d'autres systèmes à interaction hiérarchique. Par exemple, si vous numérisez des échantillons de musique de différents styles (rock, jazz, classique), vous trouverez que la distribution de leurs spectres de puissance est très proche d'un bruit 1/f.
4. Utilisez la fonction lcorr pour comparer la structure statistique de ce bruit avec celle du bruit blanc généré ci-dessus en calculant leurs autocorrélations.
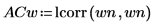
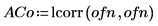
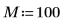
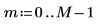
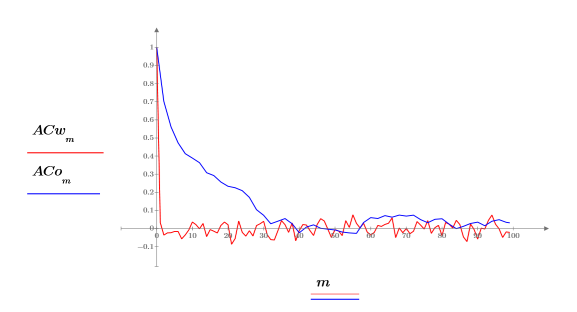
Contrairement au bruit blanc, le bruit généré par onefn est corrélé, avec la corrélation diminuant lorsque le retard augmente.
Comparaison des signaux de bruit à l'aide des spectres de puissance
Une autre manière d'analyser les différences entre le bruit blanc et le bruit 1/f est de comparer leurs spectres de puissance.
1. Supposez 50 cellules de groupes de fréquences de 20.
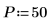
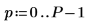
2. Utilisez les fonctions mag et dft pour calculer l'amplitude des spectres de fréquence pour chaque signal.
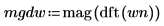
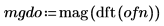
3. Lissez le résultat en moyennant sur les groupes de fréquences.
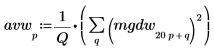
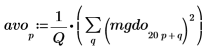
4. Tracez le spectre de bruit blanc.
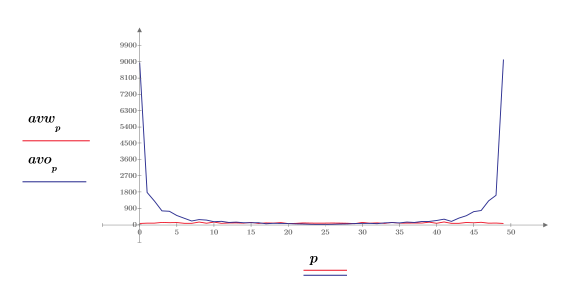
Comme prévu, le spectre de bruit blanc est essentiellement plat. Le spectre d'amplitude de l'approximation 1/f diminue rapidement avec l'augmentation de la fréquence.
5. Utilisez la fonction log pour calculer le logarithme plus représentatif de l'amplitude.
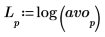
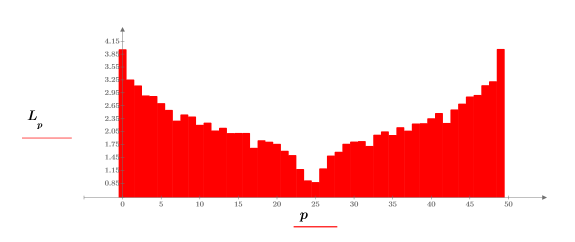
Expérience
En guise d'expérience, essayez de construire un spectre de puissance 1/f, avec des phases aléatoires, puis prenez-en la transformée inverse afin d'obtenir le vecteur de bruit.
1. Définissez la largeur du spectre.
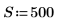
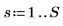
2. Utilisez la fonction exp pour construire la première moitié de la transformée. Le spectre de puissance 1/f correspond à un spectre d'amplitude de 1/sqrt(f).
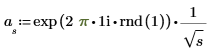
3. Calculez la seconde moitié de la transformée (pour un signal réel, cette seconde moitié est symétrique conjuguée autour du point médian).
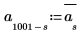
4. Définissez la moyenne du bruit à zéro.
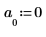
5. Utilisez la fonction idft pour obtenir la transformée de Fourier inverse (transformée relative au domaine temporel).
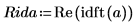
6. Tracez les valeurs réelles de la transformée inverse.
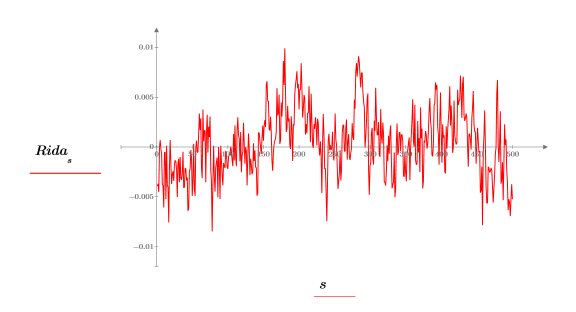
7. Utilisez la fonction lcorr pour calculer la courbe d'autocorrélation.
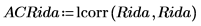
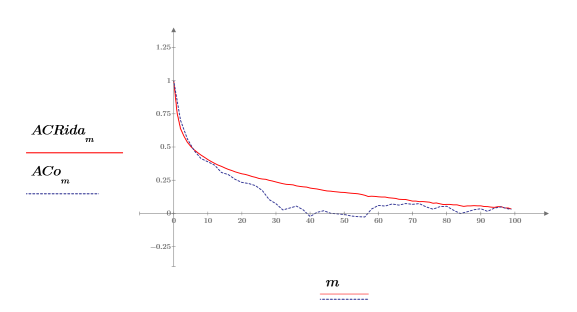
Le comportement de l'autocorrélation est similaire à la sortie de onefn, avec une corrélation de 1.0 à 0 et différents degrés de corrélation à d'autres points.