Fonctions > Vecteur et matrice > Factorisation de matrices > Exemple : Factorisation de matrice QR
Exemple : Factorisation de matrice QR
Utilisez la fonction QR pour effectuer la factorisation de matrice QR.
* 
• Pour éviter les incohérences lors de comparaisons booléennes, activez Egalité approximative dans la liste déroulante Options de calcul.
• L'exemple utilise une matrice complexe comme entrée, mais la fonction accepte aussi une matrice réelle comme entrée.
Factorisation QR avec pivotement
1. Définissez une matrice réelle M1 de dimensions m x n de sorte que m > n.
Cliquez pour copier cette expression
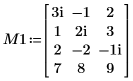
2. Définissez l'argument p pour contrôler l'activation/la désactivation du pivotement.
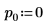
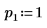
Cliquez pour copier cette expression
Cliquez pour copier cette expression
3. Utilisez la fonction QR pour effectuer la factorisation de matrice QRM1.
Cliquez pour copier cette expression
* 
La fonction par défaut QR(M1) est équivalente à QR(M,1).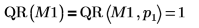
Cliquez pour copier cette expression
4. Affichez que M1 x P1 = Q1 x R1.
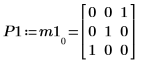
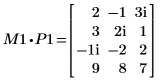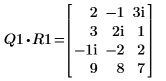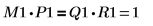Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation est logiquement vraie.
5. Utilisez la fonction submatrix pour extraire la matrice M2, comme m < n, puis appliquez la fonction QR.
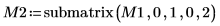
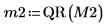
Cliquez pour copier cette expression
Cliquez pour copier cette expression
6. Affichez que M2 x P2 = Q2 x R2.
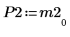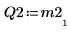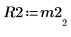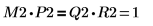Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation est logiquement vraie.
7. Utilisez la fonction submatrix pour extraire la matrice M3, de sorte que m = n, puis appliquez la fonction QR.
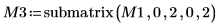
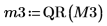
Cliquez pour copier cette expression
Cliquez pour copier cette expression
8. Affichez que M3 x P3 = Q3 x R3.
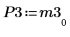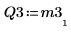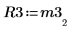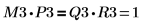Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation est logiquement vraie.
Factorisation QR sans pivotement
1. Désactivez le pivotement puis appliquez la fonction QR à la matrice M1 (m > n).
Cliquez pour copier cette expression
2. Affichez que M1 = Q10 x R10.
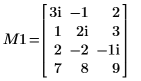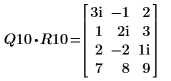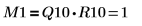Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation est logiquement vraie.
3. Désactivez le pivotement puis appliquez la fonction QR à la matrice M2 (m < n).
Cliquez pour copier cette expression
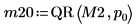
4. Affichez que M2 = Q20 x R20.
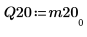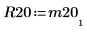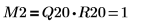Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation est logiquement vraie.
5. Désactivez le pivotement puis appliquez la fonction QR à la matrice M3 (m = n).
Cliquez pour copier cette expression
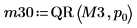
6. Affichez que M3 = Q30 x R30.
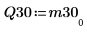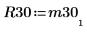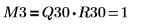Cliquez pour copier cette expression
Cliquez pour copier cette expression
Cliquez pour copier cette expression
La relation est logiquement vraie.
A propos des fonctions de factorisation de matrice
Est-ce que cela a été utile ?