Exemple : Factorisation de Cholesky des matrices complexes

Fonctions > Vecteur et matrice > Factorisation de matrices > Exemple : Factorisation de Cholesky des matrices complexes

Utilisez la fonction Cholesky pour effectuer la factorisation Hermitian d'une matrice Cholesky complexe.

Pour éviter les incohérences lors de comparaisons booléennes, activez Egalité approximative dans la liste déroulante Options de calcul.

1. Définissez une matrice carrée définie Hermitian complexe M.

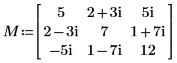
2. Appliquez la fonction eigenvals pour vous assurer que la matrice est positive définie.

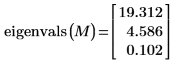
3. Définissez les arguments p et u pour contrôler l'activation/la désactivation du pivotement et la factorisation inférieure/supérieure.

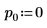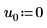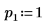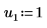4. Utilisez la fonction Cholesky pour effectuer la factorisation par défaut de la matrice M, avec pivotement et factorisation inférieure.

La fonction par défaut Cholesky(M) est équivalente à Cholesky(M,1,0)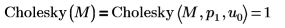

<region id="ID0E2P3EB" actualWidth="284.50666666666672" actualHeight="27.791200000000003" top="729.60000000000014" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="76">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </math>
</region>

5. Montrez que P10T x M x P10 = L10 x conj(L10T).

<region id="ID0E2S3EB" actualWidth="165.17000000000002" actualHeight="62.800000000000004" top="825.60000000000014" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="78"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>0</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EJT3EB" actualWidth="371.56" actualHeight="62.800000000000004" top="902.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="80"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>1</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>
<region id="ID0E3T3EB" actualWidth="286.33333333333331" actualHeight="62.800000000000004" top="979.20000000000016" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="82"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>	<region id="ID0EKU3EB" actualWidth="273.75666666666666" actualHeight="62.800000000000004" top="1056.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="84"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <conjugate /> <parens> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </parens> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>
<region id="ID0E4U3EB" actualWidth="230.72333333333333" actualHeight="31.752000000000002" top="1113.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="86"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <conjugate /> <parens> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </parens> </apply> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>

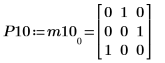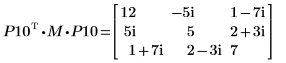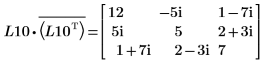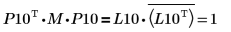La relation est logiquement vraie.

6. Utilisez la fonction Cholesky pour effectuer la factorisation par défaut de la matrice M, sans pivotement ni factorisation inférieure (par défaut).

<region id="ID0ECX3EB" actualWidth="458.07000000000011" actualHeight="62.800000000000004" top="1248.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="88">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m00</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

Ne pas spécifier d'argument u, comme dans Cholesky(M, 0), équivaut à la définir sur 0 comme dans Cholesky(M, 0, 0).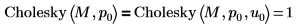

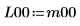
<region id="ID0E2Y3EB" actualWidth="307.08666666666676" actualHeight="27.791200000000003" top="1344.0000000000002" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="90">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id xml:space="preserve">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

Lorsque le pivotement est activé, la matrice inférieure renvoyée, L10, n'est PAS égale à la matrice inférieure renvoyée, L00, lorsqu'il est désactivé.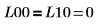

La relation est logiquement fausse.

7. Montrez que M = L00 x conj(L00T).

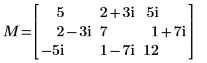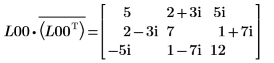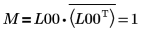La relation est logiquement vraie.

8. Utilisez la fonction Cholesky pour effectuer la factorisation de la matrice M, avec pivotement et factorisation supérieure.

<region id="ID0E6B4EB" actualWidth="452.76666666666671" actualHeight="118.60000000000001" top="1939.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="102">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m11</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

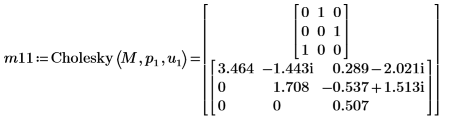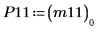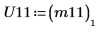9. Montrez que P11T x M x P11 = conj(U11T) x U11.

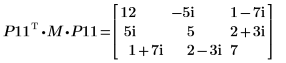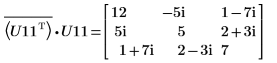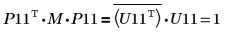La relation est logiquement vraie.

10. Utilisez la fonction Cholesky pour effectuer la factorisation de la matrice M, sans pivotement ni factorisation supérieure.

<region id="ID0EIJ4EB" actualWidth="478.01333333333338" actualHeight="62.800000000000004" top="2457.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="114">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m01</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

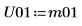
11. Montrez que M = conj(U01T) x U01.

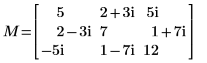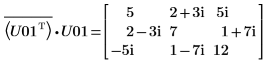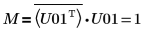La relation est logiquement vraie.

Rubriques associées

A propos des fonctions de factorisation de matrice

Est-ce que cela a été utile ?