Exemple : Transformée inverse idft
La fonction idft correspond à la transformée inverse de dft et doit donc rétablir l'entrée des données d'origine dans la transformée complexe.
Utilisation de vecteurs (1D)
1. Définissez la longueur du vecteur v.
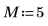
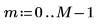
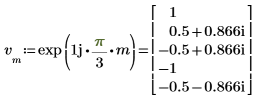
3. Utilisez la fonction dft pour calculer la transformée de Fourier ascendante de v.
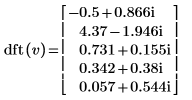
4. Utilisez la fonction idft pour calculer la transformée inverse de v.

5. Démontrez que la transformée inverse de la transformée ascendante du vecteur v est le vecteur d'origine v.
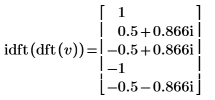 |  |
Les résultats sont identiques.
Utilisation de Matrices (2D)
1. Définissez et évaluez la matrice C.
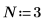
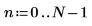
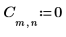
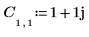
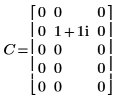
2. Utilisez la fonction dft pour calculer la transformée ascendante de la matrice C.

3. Utilisez la fonction idft pour calculer la transformée inverse de la matrice C.

4. Démontrez que la transformée inverse de la transformée ascendante de la matrice C est la matrice d'origine C.
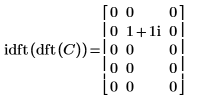 | 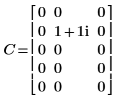 |
Les résultats sont identiques.
Démonstration de la somme idft somme sous-jacente
Cas unidimensionnel :
1. Utilisez la fonction exp et l'opérateur de somme pour calculer la transformée inverse de la matrice v.
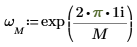
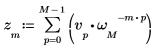
2. Comparez la transformée ascendante qui résulte du vecteur v avec la sortie de la fonction dft.
 | 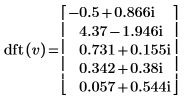 |
Les résultats sont identiques.
3. Utilisez l'opérateur de somme pour calculer la transformée inverse du vecteur v.
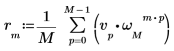
4. Comparez la transformée inverse qui résulte du vecteur v avec la sortie de la fonction idft.
 |  |
Les résultats sont identiques.
Cas bidimensionnel :
1. Utilisez la fonction exp et l'opérateur de somme pour calculer la transformée ascendante de la matrice C.
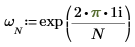
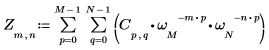
2. Comparez la transformée ascendante qui résulte de la matrice C avec la sortie de la fonction dft.


Les résultats sont identiques.
3. Utilisez l'opérateur de somme pour calculer la transformée inverse du vecteur C.
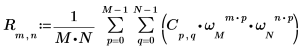
4. Comparez la transformée inverse qui résulte de la matrice C avec la sortie de la fonction idft.


Les résultats sont identiques.