Ejemplo: dft de transformada directa
Utilice la función dft para buscar la transformada de Fourier compleja de un vector o de una matriz con valores reales o complejos de cualquier tamaño, con un tiempo o espacio constante entre muestras.
Datos sinusoidales complejos unidimensionales
Cree un conjunto de datos complejo simulado con N puntos de datos en el espaciado de muestra T.
1. Defina el número de puntos de datos.
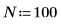
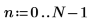
2. Defina el tiempo T en que se recopilan las muestras.
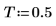
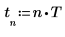
3. Defina una frecuencia angular.
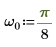
4. Utilice la función exp para definir una función exponencial.
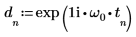
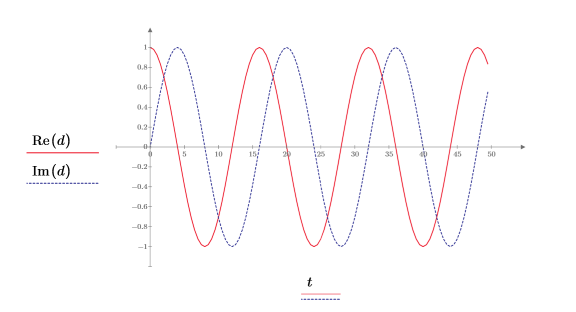
5. Utilice las funciones Re e Im para extraer y trazar los componentes reales e imaginarios como funciones de tiempo.
6. Aplique la función dft para transformar los datos en el dominio de frecuencias.
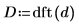
7. Recopile los valores absolutos de D en un array nuevo.
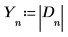
8. Defina la frecuencia de muestreo y la frecuencia correspondiente a la entrada de orden n en el vector transformado.
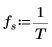
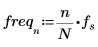
9. Utilice las funciones match y max para buscar el valor máximo y la frecuencia correspondiente dentro de la señal transformada.
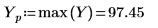
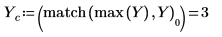
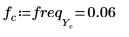
10. Trace el vector transformado y utilice marcadores verticales y horizontales para marcar la frecuencia en que la amplitud se encuentra en su valor máximo.
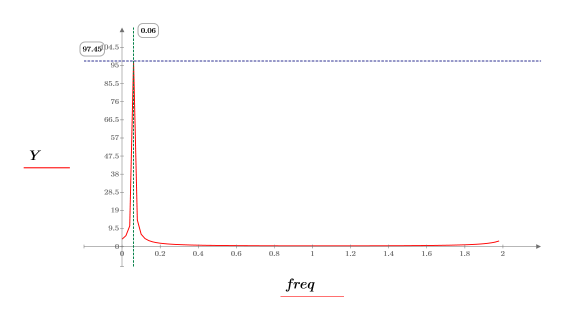
◦ La mitad superior de las muestras de dominio de frecuencias representa las frecuencias negativas.
◦ Esta señal compleja no tiene contenido de frecuencia negativo.
Información adicional
• Para el vector de datos reales v, el vector dft(v) es, en general, complejo y conjugado simétrico en el valor medio. En el caso de una matriz real, cada columna del resultado es conjugada simétrica.
• En el caso de una entrada de array cuadrado A, dft(A) es simétrico.
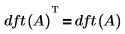
• Según el teorema de muestreo de Nyquist, la frecuencia de muestreo debe ser al menos el doble de la frecuencia más alta que desea que resuelva la transformada de Fourier.
• El algoritmo divisor de número primo que se utiliza en la transformada rápida de Fourier se ralentiza cuando el número de puntos de datos es un número primo elevado. Es posible que nunca se encuentre con este problema, pero téngalo en cuenta si va a trabajar con números primos muy grandes de puntos de datos.