Solving ODEs
You can use solve blocks, and the odesolve function, to find a function that satisfies an Ordinary Differential Equation (ODE) over a given range of values.
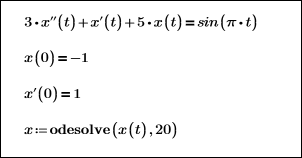
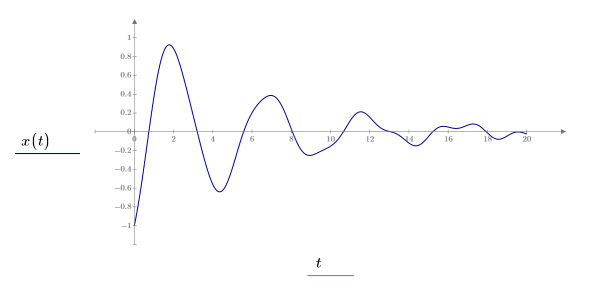
Here, the output function is solved over the range 0 ≤ x ≤ 20:
When using the ODE in solve blocks, you must pay attention to the following constraints:
• Operators—Use the equal to operator in solve blocks for solving ODEs. Do not use the comparison operators or the inequality operator. For defining derivatives, use the derivative or the prime operator, such as d/dx and d2/dx2 or y'(x) and y''(x).
• Initial and Boundary Conditions—For a single nth order ODE, there must be n independent equality constraints:
◦ Initial value problem—The values of y(x) and of its first n − 1 derivatives at a single initial point a are required.
◦ Boundary value problem— The n constraints must specify certain values of y(x) and its derivatives at the initial point a or the terminal point b. The constraints must satisfy the requirements for the inputs to the sbval function. Function odesolve calls sbval when you provide boundary value conditions.
In each case, the endpoints you use in boundary conditions must match the endpoints specified in the odesolve command. PTC Mathcad checks for the correct type and number of conditions and returns an error if there is a mistake.
• Algebraic constraints—You can add algebraic constraints, such as y(b) + z(b) = w(b). The solve block then contains an extra unknown function, w, that you must specify as one of the output functions in odesolve.
• Output—You must assign the output of odesolve either to a function name or to a vector of function names, without arguments.
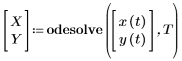
The implicit argument for these functions is the variable of integration:
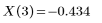
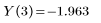
Solving Methods
• Depending on the scale of the problem and on the relative step size you use, you may need to reduce the value of TOL to get appropriate solutions. Try this when PTC Mathcadodesolve reports there are too many integrator steps.
• The functions being solved must not contain any singularities over the interval of integration. Otherwise, they can produce unreliable results.
• When solving problems with periodic behavior over many cycles, aliasing can occur. To get the expected frequencies in your results, increase the number of interpolation points.
• To solve an ODE that is not linear in the highest derivative term or to solve ODEs in a program loop, use rkfixed or one of the other command-line ODE solvers. You can also assign the output of a parameterized solve block in a program loop using local functions.