Deriving Initial Conditions for an ODE
The following functions are used with boundary-value problems, where not all initial conditions are known.
• bvalfit(v1, v2, x1, x2, xf, D, load1, load2, scoreb)
• sbval(v1, x1, x2, D, load1, scorei)
Returns a vector containing those initial values left unspecified at x1 for the ODE or system of ODEs identified in D. These initial values can then be used in one of the ODE solvers. If you know some values of the solution and its first n − 1 derivatives at an intermediate value, use bvalfit which is especially useful when the derivative has a discontinuity somewhere in the integration interval. If you know some values at the initial and terminal points, use sbval. The boundary value problem is converted to an initial value problem by shooting from the endpoints and matching the trajectories of the solution and its derivatives at an intermediate point.
Arguments
• v1, v2 are vectors of real guesses for the initial values left unspecified at x1.
• x1, x2 are the real endpoints of the interval on which the solution to differential equations is evaluated.
• xf is a real intermediate point between x1 and x2 at which the trajectories of the solutions are constrained to be equal.
• D(x, y) is an n element vector-valued function of the independent variable, x, and a vector of functions, y, containing the equations for the first derivatives of all unknown functions in the system of ODEs.
To create this vector, cast your equations with a first derivative term by itself on the left-hand-side, with no multipliers, and no higher order derivatives in the equation. For example, a single ODE of the function y(x) which contains a second derivative must be written as a system of equations in y0(x) and y1(x), where the first derivative of y0 is y1. The following single-function ODE is rewritten for the solver, using vector subscripts:
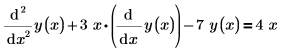
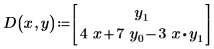 | with implied left-hand-side | 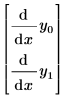 |
• load1(x1, v1), load2(x2, v2) are real vector-valued functions whose elements correspond to the values of yn at x1 and x2 respectively. Some of these values are known initial conditions. Unknown values are set to corresponding guess values from v1 and v2 respectively.
• scoreb(xf, y) is a real vector-valued function used to specify how you want the solutions to match at xf. Usually you need to define scoreb(xf, y):= y to make the solutions to all unknown functions match up at xf.
• scorei(x2, y) is a real vector-valued function having the same number of elements as v. Each element is the difference between an initial condition at x2, as originally specified, and the corresponding estimate from the solver. The score vector measures how closely a proposed solution matches the initial conditions at x2. A value of 0 for any element indicates a perfect match.