Singular Value Decomposition
• svds(A)—Returns a vector containing the singular values of A, the positive square roots of the eigenvalues of matrix AH·A, where AH is the conjugate transpose of A. You can compute AH using the transpose and complex conjugate operators as follows.
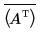
• svd(A)—Returns a vector of 3 nested arrays.
The first array contains the vector s of singular values returned by svds. The next two arrays are matrices U and VH satisfying A = U∙diag(s)·VH. The third entry VH is the conjugate transpose of V.
The third array is VH and not V. This means that the conjugate transpose has already been applied to the returned array. You do not need to apply it again. You can use the returned array directly in the formula.
Arguments
• A is an m × n array, where m ≥ n. For svd, the array elements must be real numbers; for svds, complex values are allowed.
Additional Information
• Singular values are always real and positive. Very small values should be interpreted as 0.
• The svd function uses the Intel Basic Linear Algebra Subprograms (BLAS)/Linear Algebra Package (LAPACK) libraries.