Recursive Functions
When a function name appears on both sides of the definition operator, the function is considered recursive. To write a recursive function, you must name it with a previously undefined name and label it as Function. Otherwise, PTC Mathcad does not recognize the recursive definition.
If the function is already defined as a built-in or a user-defined function, the previous definition is overwritten. For example, you can change the value of the sin function in the following way:
sin(x) := sin(x · π / 180)
This function is not recursive.
Recursive functions are useful for implementing numerical functions like the factorial function:
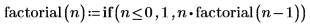
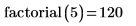
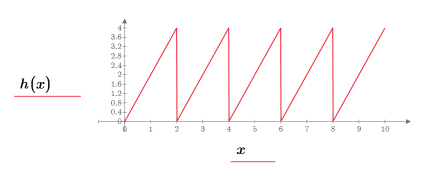
or defining arbitrary periodic functions, such as the sawtooth wave:
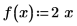 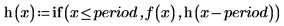 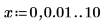 | 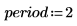 |
A recursive function definition must have at least two parts:
• An initial condition that prevents the recursion from going forever.
• A definition of the function in terms of some previous values of the function.
If you do not specify an initial condition that stops the recursion, a loop occurs and an error message appears when you try to evaluate the function.
f(x) := x · f(x − 1)