Nonlinear Regression
• genfit(vx, vy, vg, F)—Returns a vector containing the parameters that make a function F of x and n parameters u1... un best approximate the data in vx and vy.
The genfit function employs an optimized version of the Levenberg-Marquardt method for minimization. While frequently faster and less sensitive to poor guess values, this implementation may fail to converge well on problems with many local minima, such as rational functions. This implementation is sensitive to incorrect derivative vectors.
Arguments
• vx, vy are vectors of real data values of the same length, corresponding to the x and y values in the data set. There must be at least as many data points as parameters.
• vg is an n element vector of guess values for the parameters. If n = 1, then vg is a scalar.
• F(x, u) is a fitting function, or a vector of functions, where x is the independent variable and u is either a vector of parameters or individual parameter names. The following equation is both a valid representation for a fitting function:
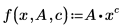
• n is a positive integer. In the case of non-vectorized parameters, there is a limit of nine individual names.
Improving Convergence
To improve convergence and possibly the accuracy of genfit, you can represent F as an n+1 vector of functions in which the first entry F0 is the fitting function f and the remaining entries F1, F2,…, Fn are the symbolic partial derivatives of f with respect to the n parameters.
In terms of the two ways of representing the fitting function shown above, you can only use f(x,A,c) if finding the partial derivatives symbolically. Thus, in representing F as a vector of functions, n has a limit of 9, so F has a maximum length of 10. You can create vector F by building a matrix of the appropriate partial derivatives and evaluating it symbolically:
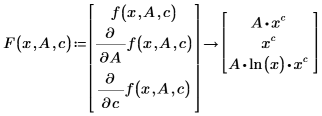
Additional Information
• You should provide only the name of the fitting function or vector of functions, without any arguments, to genfit.
• If you use the fitting function without the symbolic parameter partial derivatives, then genfit calculates the parameter partial derivatives numerically. This is less accurate than supplying the symbolic derivatives, but might be convenient in some cases.
• If genfit fails to convert, then you may wish to try other guess values or scaling your data so that all parameters are of a similar order of magnitude. As with all numerical solution techniques, nonlinear problems are highly sensitive to guess values.
• You may want to plot your fitting function with the guess values to help you refine the guess values before using genfit.
• The Optimized Levenberg-Marquardt method is more sensitive to errors in the supplied algebraic derivatives. If genfit fails, then you should check the derivative expressions.