Hypergeometric Functions

Functions > Special Functions > Other Special Functions > Hypergeometric Functions

Hypergeometric Functions

• fhyper(a, b, c, x)—Returns the value of the Gauss hypergeometric function, 2F1(a, b, c, x), or the solution of the following equation:

<region id="ID0EG5V6" top="57.600000000000009" left="38.400000000000006" height="52.369333557128911" width="346.825" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="11">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <minus />
        <apply>
          <plus />
          <apply>
            <mult />
            <apply>
              <id xml:space="preserve">x</id>
              <apply>
                <minus />
                <real>1</real>
                <id xml:space="preserve">x</id>
              </apply>
            </apply>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <mult />
            <parens>
              <apply>
                <minus />
                <id xml:space="preserve">c</id>
                <apply>
                  <mult />
                  <parens>
                    <apply>
                      <plus />
                      <apply>
                        <plus />
                        <id xml:space="preserve">a</id>
                        <id xml:space="preserve">b</id>
                      </apply>
                      <real>1</real>
                    </apply>
                  </parens>
                  <id xml:space="preserve">x</id>
                </apply>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <id xml:space="preserve">aby</id>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

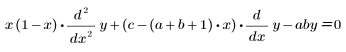
• mhyper(a, b, x)—Returns the value of the confluent hypergeometric function, 1F1(a, b, x) or M(a, b, x), or the solution of the following equation:

<region id="ID0EKAW6" top="115.20000000000002" left="38.400000000000006" height="52.369333557128911" width="220.36833333333331" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="13">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <minus />
        <apply>
          <plus />
          <apply>
            <mult />
            <id xml:space="preserve">x</id>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <real>2</real>
              </degree>
            </apply>
          </apply>
          <apply>
            <mult />
            <parens>
              <apply>
                <minus />
                <id xml:space="preserve">b</id>
                <id xml:space="preserve">x</id>
              </apply>
            </parens>
            <apply>
              <derivative />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <id xml:space="preserve">y</id>
              </lambda>
              <degree>
                <placeholder />
              </degree>
            </apply>
          </apply>
        </apply>
        <id xml:space="preserve">ay</id>
      </apply>
      <real>0</real>
    </apply>
  </math>
</region>

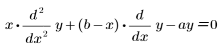
The hypergeometric functions are calculated by series expansion. Many functions are special cases of the hypergeometric functions. Examples of hypergeometric functions include the Legendre polynomials and the following functions:

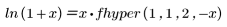
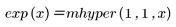
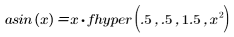
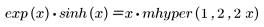
Arguments

• a, b and c are real, dimensionless scalars. If a and b are nonzero, c must also be nonzero.

• x is a real, dimensionless scalar. For fhyper, −1 < x < 1.

Related Topics

About Other Special Functions

Polynomial Functions

Was this helpful?