Exponential Integrals

Functions > Symbolic Functions > Exponential Integrals

Exponential Integrals

• Ei(x)—Returns the exponential integral function (Cauchy principal value) of x, which is defined as follows:

Click to copy this expression

<region id="ID0EJCACB" top="115.20000000000002" left="57.600000000000009" height="80.552" width="118.27166666666668" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="7">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <id xml:space="preserve">Ei</id>
        <id xml:space="preserve">x</id>
      </apply>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve">e</id>
              <id xml:space="preserve">t</id>
            </apply>
            <id xml:space="preserve">t</id>
          </apply>
        </lambda>
        <lowerBound>
          <apply>
            <neg />
            <id xml:space="preserve" labels="CONSTANT">∞</id>
          </apply>
        </lowerBound>
        <upperBound>
          <id xml:space="preserve" labels="CONSTANT">π</id>
        </upperBound>
      </apply>
    </apply>
  </math>
</region>

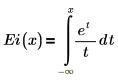
Ei(x) returns only the real part of the complex exponential integral function.

For x > 0, the integral is interpreted as the Cauchy principal value.

• Ei(n, x)—Returns the generalized exponential integral function of x.

For an arbitrary integer n, Ei(n, x) is defined by the recurrence relation:

<region id="ID0E6EACB" top="307.20000000000005" left="57.600000000000009" height="27.752000000000002" width="229.48666666666668" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="13">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <mult />
        <id xml:space="preserve">n</id>
        <apply>
          <id xml:space="preserve">Ei</id>
          <sequence>
            <apply>
              <plus />
              <id xml:space="preserve">n</id>
              <real>1</real>
            </apply>
            <id xml:space="preserve">x</id>
          </sequence>
        </apply>
      </apply>
      <apply>
        <minus />
        <apply>
          <pow />
          <id xml:space="preserve">e</id>
          <apply>
            <neg />
            <id xml:space="preserve">x</id>
          </apply>
        </apply>
        <apply>
          <mult />
          <id xml:space="preserve">x</id>
          <apply>
            <id xml:space="preserve">Ei</id>
            <sequence>
              <id xml:space="preserve">n</id>
              <id xml:space="preserve">x</id>
            </sequence>
          </apply>
        </apply>
      </apply>
    </apply>
  </math>
</region>

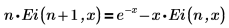
For the case of n = 1, Ei(n, x) is defined as follows:

<region id="ID0E2FACB" top="249.60000000000002" left="57.600000000000009" height="50.000000000000007" width="242.08666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="11">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <neg />
        <apply>
          <id xml:space="preserve">Ei</id>
          <sequence>
            <real>1</real>
            <apply>
              <neg />
              <id xml:space="preserve">x</id>
            </apply>
          </sequence>
        </apply>
      </apply>
      <apply>
        <plus />
        <apply>
          <plus />
          <id xml:space="preserve" labels="CONSTANT">γ</id>
          <apply>
            <id xml:space="preserve">ln</id>
            <apply>
              <neg />
              <id xml:space="preserve">x</id>
            </apply>
          </apply>
        </apply>
        <apply>
          <summation />
          <lambda>
            <boundVars>
              <id xml:space="preserve">k</id>
            </boundVars>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <id xml:space="preserve">k</id>
              </apply>
              <apply>
                <mult />
                <id xml:space="preserve">k</id>
                <apply>
                  <factorial />
                  <id xml:space="preserve">k</id>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>1</real>
          </lowerBound>
          <upperBound>
            <id xml:space="preserve">∞</id>
          </upperBound>
        </apply>
      </apply>
    </apply>
  </math>
</region>

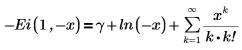
where γ is Euler's constant.

For a real number x, Ei(x) and Ei(n, x) are related to each other as follows:

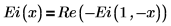
Arguments

• x is a real scalar, a vector, or a square matrix. When using the generalized exponential integral function, x can also be complex scalar.

• n is a real or complex scalar.

Related Topics

About Symbolic Functions

Example: Symbolic Integral Functions

Was this helpful?