Example: Variance and Standard Deviation

Functions > Statistics > Descriptive Statistics > Example: Variance and Standard Deviation

Use the Var and Stdev functions to compare the spread of a Weibull and a normal distribution.

1. Define data sets following a Weibull and a normal distribution.

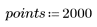
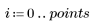
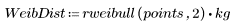
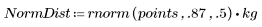
2. Plot the distributions.

<region id="ID0EWCGAB" top="312" left="0" width="626" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="0">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="1">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>NormHist</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <id label="Unit" xmlns="http://schemas.mathsoft.com/math50">kg</id>
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>WeibHist</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <id label="Unit" xmlns="http://schemas.mathsoft.com/math50">kg</id>
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="2" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>NormHist</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>WeibHist</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

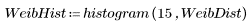
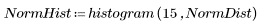
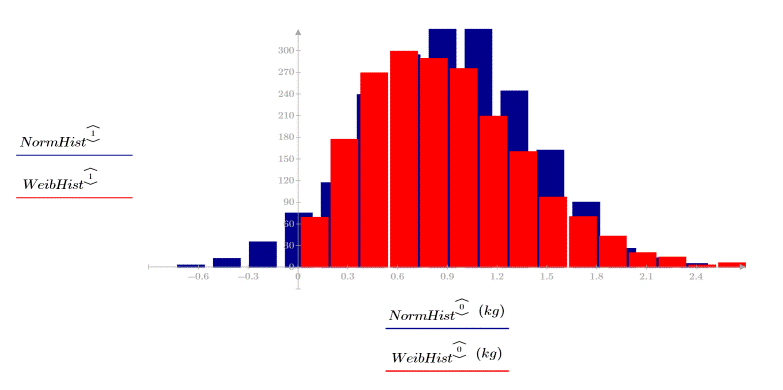
The two data sets have different spreads and shapes, even though they have similar means:

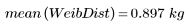
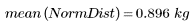
3. Calculate the sample variance of the distributions.

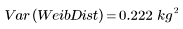
The smaller variance of the Weibull distribution indicates that it is less spread than the normal distribution.

The sample variance is calculated as follows:

<region id="ID0EKGGAB" top="1080" left="24" width="394.69" height="67.2973333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None">Variance</id>
        <boundVars>
          <id label="None">V</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <minus />
            <apply>
              <id>rows</id>
              <id>V</id>
            </apply>
            <real>1</real>
          </apply>
        </apply>
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id>i</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id>V</id>
                      <id>i</id>
                    </apply>
                    <apply>
                      <id>mean</id>
                      <id>V</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <apply>
                  <id>rows</id>
                  <id>V</id>
                </apply>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" />
    </resultFormat>
  </math>
</region>

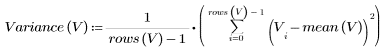
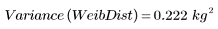
4. Calculate the sample standard deviation of the Weibull distribution.

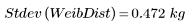
The standard deviation has the same units as those of the original data, making it a slightly more intuitive measure of the dispersion than the variance. It can be considered a measure of the error in a series of measurements that should really be identical.

The sample standard deviation is the square root of the sample variance:

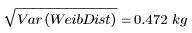
5. Calculate the population variance and standard deviations for the Weibull distribution:

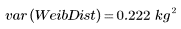
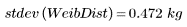
The population variance and standard deviation are divided by the sample size, and not by the sample size minus one:

<region id="ID0EOLGAB" top="1584" left="24" width="369.073333333333" height="67.2973333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None">variance</id>
        <boundVars>
          <id label="None">V</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <id>rows</id>
            <id>V</id>
          </apply>
        </apply>
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id>i</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id>V</id>
                      <id>i</id>
                    </apply>
                    <apply>
                      <id>mean</id>
                      <id>V</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <apply>
                  <id>rows</id>
                  <id>V</id>
                </apply>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" />
    </resultFormat>
  </math>
</region>

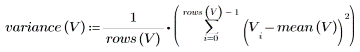
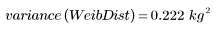
The sample variance, or function Var, is the more commonly used definition in quantitative data analysis.