Example: Using Units with the Polynomial Interpolation Functions

Functions > Data Analysis > Interpolation and Prediction > Example: Using Units with the Polynomial Interpolation Functions

1. Define two input vectors and an independent variable.

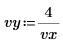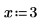2. Define the units.

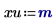
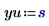
3. Evaluate the input vectors and the input variable.

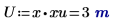The unit of the independent variable U must match the unit of the first argument vector.

Polynomial Interpolation

1. Use the polyint function to evaluate the interpolation function at the specified independent variable values.

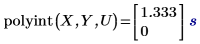
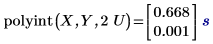
Looking up U in input vector X results in a match and the corresponding exact value in vector Y is 1.333 with an error of zero. However, 2U has no exact match in X and this results in an interpolated value with a none-zero error.

2. Use function length to determine the length of the input vectors, then create a short program to evaluate the interpolation functions at different points. Display the interpolated points in the first column and the error values in the second column.

<region id="ID0EVPCU" actualWidth="485.86333333333334" actualHeight="197.304" top="1075.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="45">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <eval>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L</id>
 </range>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>1</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </program>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

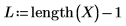
Variable u must be a scalar, and the unit m is added as part of the function argument.

3. Save the interpolation points and the error values into two separate vectors.

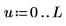
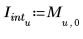
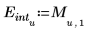
4. Plot the interpolation points along with the error envelope.

<region id="ID0E5TCU" actualWidth="576" actualHeight="307.2" top="1401.6000000000001" left="38.400000000000006" height="307.2" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="49">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="50">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace resultRef="51">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="418.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="52">
 <real xmlns="http://schemas.mathsoft.com/math50">0.9</real>
 </secondTickValue>
 <endValue resultRef="53">
 <real xmlns="http://schemas.mathsoft.com/math50">9</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="126.556666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

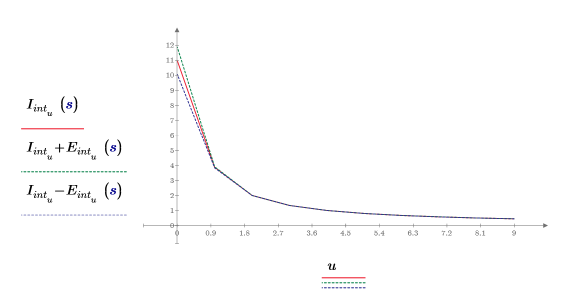
The error starts out relatively large then becomes negligent after the second interpolation point.

Polynomial Iteration

1. Use the polyiter function to evaluate the iteration function at the specified independent variable value, the number of maximum iterations and the tolerance.

<region id="ID0EDWCU" actualWidth="261.85" actualHeight="62.800000000000004" top="1900.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="54">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>2</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0ERWCU" actualWidth="261.85" actualHeight="62.800000000000004" top="1977.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="55">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>5</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

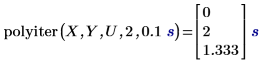
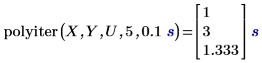
• The algorithm stops if the last two iterated estimates of the data point agree to within the tolerance value, or if the number of iterations reaches the maximum allowed number of iterations.

• The first result shows that the iteration function failed to converge after reaching the maximum allowed number of two iterations, so it returned the corresponding element in vector Y.

• The second result shows that the iteration function converged after the third iteration and it did not reach the maximum allowed number of five iterations.

2. Use a short program to evaluate the iteration function at ten different points. Use function augment to add the error value in the fourth column of the returned matrix which displays the merge status in the first column, the number of utilized iterations in the second column, and the iterated values in the third column.

<region id="ID0EF3CU" actualWidth="487.13666666666654" actualHeight="200.2" top="2284.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="56">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">
 P<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">ord</id>
 <id labels="VARIABLE" xml:space="preserve">err</id>
 </boundVars>
 </function>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">order</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ord</id>
 </localDefine>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">error</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">err</id>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <apply>
 <minus />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">length</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 </apply>
 <real>1</real>
 </apply>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">K</id>
 <id labels="*" xml:space="preserve">u</id>
 </apply>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>2</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">N</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">order</id>
 <apply>
 <scale />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve">s</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">Z</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">augment</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 </sequence>
 </apply>
 </localDefine>
 <return>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Z</id>
 </return>
 </program>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

3. Save the interpolation points and the error values into separate vectors.

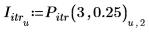
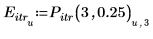
4. Plot the iteration points for 3 iterations and an error of 0.25.

<region id="ID0EU6CU" actualWidth="577" actualHeight="307.20000000000005" top="2707.2000000000003" left="38.400000000000006" height="307.20000000000005" width="577" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="59">
 <traceStyle color="#FFED1D2F" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="60">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace resultRef="61">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="419.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="bottom" positionticmark="-1" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>10</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="62">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0.25" end="3.55">
 <axisLine position="origin" positionticmark="0" legendWidth="123.37" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

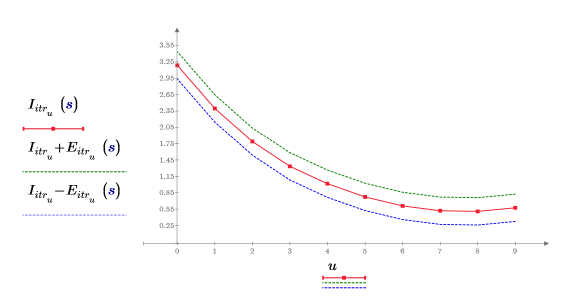
The error is constant at every interpolation point.

5. Compare the returned results of interpolation and iteration when the maximum number of iterations is set to 3 and the error is set to 0.25.

<region id="ID0EIBDU" actualWidth="576.60000000000014" actualHeight="287.99999999999994" top="3129.6000000000004" left="38.400000000000006" height="287.99999999999994" width="576.60000000000014" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="63">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="64">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="81.1466666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

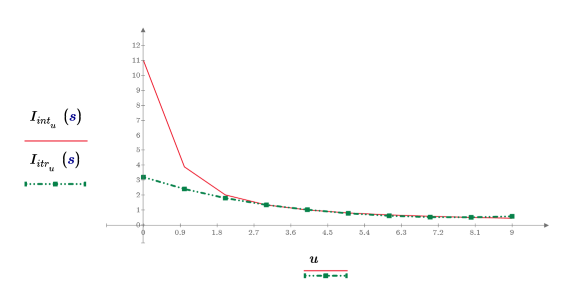
6. Show that the result of interpolation is identical to the result of iteration when the number of iterations is set to a large number and the error is set to zero.

<region id="ID0EGDDU" actualWidth="576.6" actualHeight="288" top="3571.2000000000007" left="38.400000000000006" height="288" width="576.6" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="66">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="67">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="87.5333333333333" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I0<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

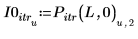
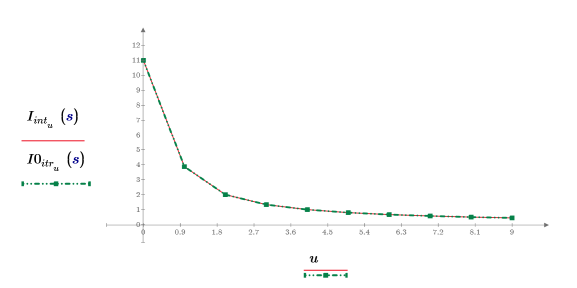
The maximum number of iterations must be less than the length of the input vectors.