Example: Using the Limit Operator
Using Infinity as a Limiting Value
1. Use the limit operator and symbolically evaluate an expression as its argument approaches infinity.
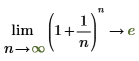
2. Plot the function to facilitate its visualization. Use a horizontal marker to represent e.
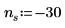 | 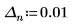 | 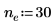 |
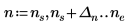 | ||
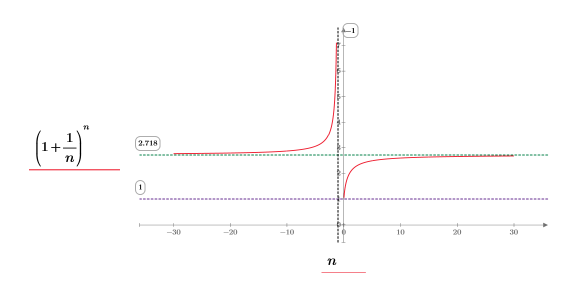 | ||
In the (x, y) quadrant we observe the following:
◦ As n approaches positive infinity, the function approaches y=e.
◦ As n approaches 0, the function approaches y=1.
Mathematically, this is represented by the following symbolic evaluations:
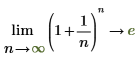 | 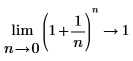 |
In the (-x, y) quadrant we observe the following:
◦ As n approaches negative infinity, the function approaches y=e.
◦ As n approaches -1, the function approaches y=infinity.
Mathematically, this is represented by the following symbolic evaluations:
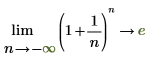 | 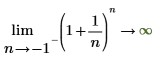 |
The use of Left-hand Limit-side in the second equation means that the -1 is to be approached from the left-side of the curve. If this is not specified, then the evaluation returns "undefined" because the function is not defined for -1 < n < 0: 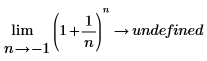 |
Using the Limit Side
1. Plot the cot function.
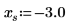 | 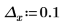 | 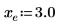 |
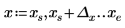 | ||
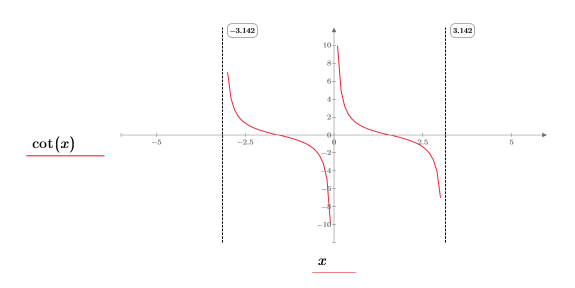 | ||
In the (x, y) quadrant we observe the following:
◦ As x approaches 0, the function approaches y=infinity.
◦ As x approaches π, the function approaches y=-infinity.
Mathematically, this is represented by the following symbolic evaluations:
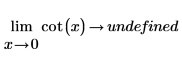 | 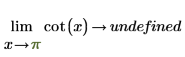 |
Since the function is symmetric around x=+/- n*π/2, the symbolic evaluation returns "undefined" because the function around x=0 (and any multiple number of π) can be either infinity or -infinity, depending on the side from which x approaches 0.
This is a good case for specifying the "Limit Side".
2. Specify the "Limit Side" and symbolically reevaluate the cot function around 0 and π.
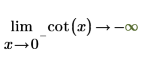 | 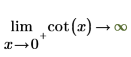 |
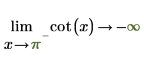 | 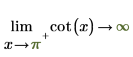 |
The returned results agree with the plot.
Sometimes it helps to plot a function in order to visualize it and to double check the validity of symbolic evaluation results. |