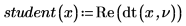Example: T-Score of a Vector of Data
Compute a t-score for a vector of normally distributed data with respect to a specified mean.
1. Define a vector of data to analyze.

2. Collect the sample statistics.
Number of samples | 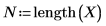 | 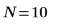 |
Sample mean | 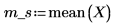 | 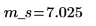 |
Sample standard deviation | 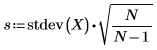 | 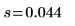 |
Standard error of the mean | 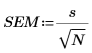 | 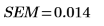 |
Degree of freedom | 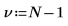 | 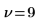 |
3. Define the significance level and the proposed population mean.
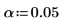
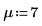
4. Calculate the t-score.
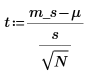
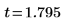
5. State the null and the alternative hypothesis.
H0: m ≤ μ
H1: m > μ
6. Calculate the p-value and test the hypothesis.
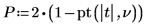
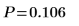
There is a 0.106 probability that the test statistic is greater than the one observed, assuming that the null hypothesis is true. The comparison between the p-value and the significance level indicates there is no evidence that the alternative hypothesis is true.
7. Calculate the limit of the critical region and test the hypothesis.
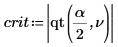
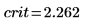
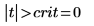
Accept the null hypothesis. There is no evidence that the mean is greater than μ.
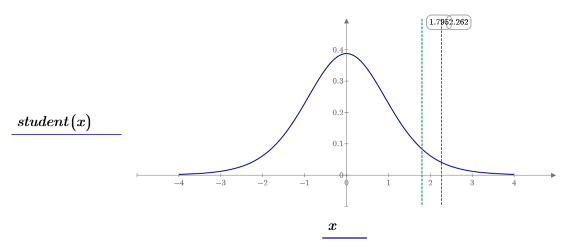
8. Plot the Student's t-distribution (blue), the boundary of the critical region (red), and the t-score (green).