Example: Thiele Interpolation
Perform Thiele continued fraction interpolation on a data set.
Thielecoeff and Thiele
Use the Thielecoeff and the Thiele function to interpolate a data set coming from a rational function.
1. Define the number of interpolation points.
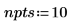
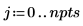
2. Define a rational function, such as the Lorentzian function.
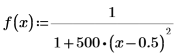
3. Take samples of the function and record their x and y values into vectors.
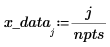
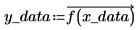
4. Use the Thielecoeff function to find the coefficients of the continued fraction that fits the sampled points.
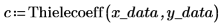
5. Call the Thiele function to perform the interpolation.
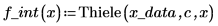
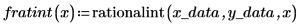
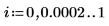
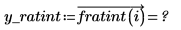
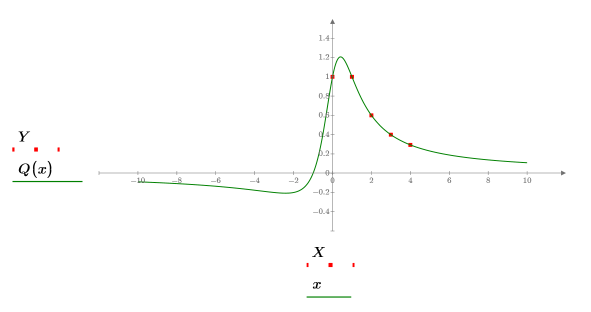
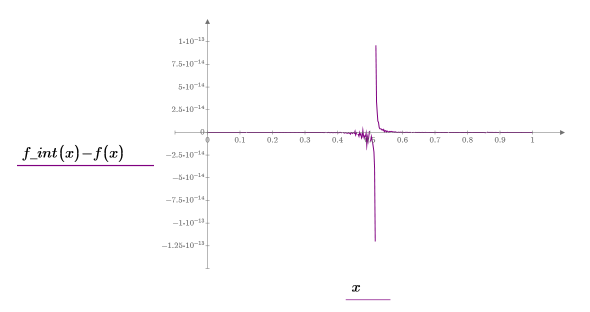
The Thiele functions work, but the rationalint function fails at some points in this interpolation range. This is because the data is symmetrical, causing divide-by-zero errors at some intermediate x values:
6. Plot the original function, the sampled points, and the interpolated curve.
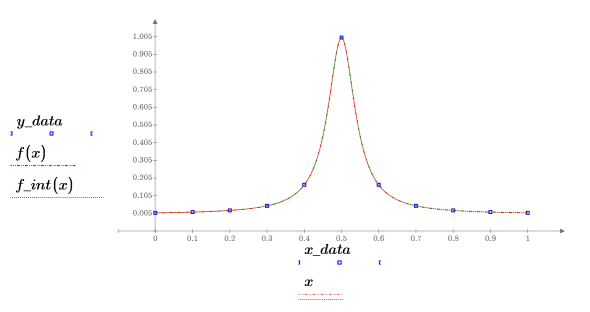
7. Plot a graph showing the residuals for the Thiele interpolation.
Order of Points
The algorithm fails to return the right values if two adjacent points have identical y values. You need to reorder the data to get the correct result.
1. Define a set of points.
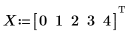
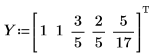
2. Find the coefficients of the Thiele function.
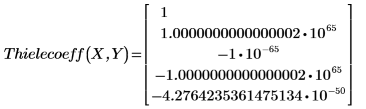
The coefficients are too large.
3. Reorder the data to get an appropriate solution.
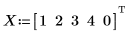
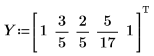
4. Repeat step 2.
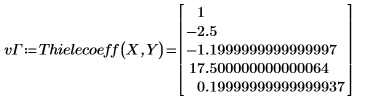
5. Define the interpolated function.
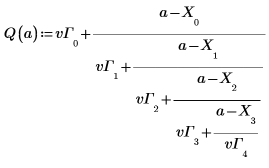
6. Plot the interpolated function and the original data points.