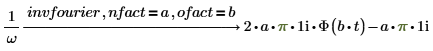Example: Symbolic Transforms
Perform symbolic Fourier, Laplace, and z transforms, and their inverses.
Fourier and Inverse Fourier Transforms
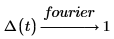
As expected, this returns a constant frequency.
2. Find the Fourier transform of a function involving the Heaviside step function Φ.
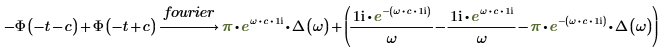
3. Add the simplify keyword to simplify the result.
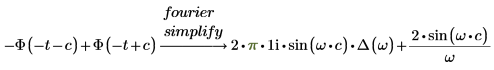
Z and Inverse Z Transforms
1. Use the keyword ztrans to calculate the z-transform of the following two functions:
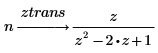
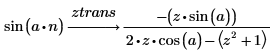
2. Use the keyword invztrans to calculate the inverse z-transform of the following two functions:
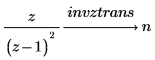
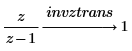
Changing the Default Variable for a Transform
1. Find the inverse Laplace of a function.
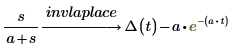
2. Change the default variable, t, in the function returned by the inverse Laplace transform by adding a pair of arguments after the transform keyword.
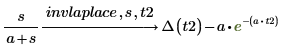
◦ The first argument, s, is the independent variable for the domain function.
◦ The second argument, t2, is the new independent variable for the transformed function.
◦ The returned inverse Laplace transform uses the variable t2 as the independent variable. Δ is the Dirac Delta function.
◦ Although you cannot evaluate Δ using the numerical equal sign, you can evaluate it using the symbolic evaluation operator.
3. Find the Laplace transform of the result, using the keyword laplace.
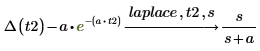
Using More Than One Keyword at a Time
If the results of a symbolic calculation are not in the form that you want, you can add a keyword after the transform keyword to modify the format of the result.
1. Find the z-transform of a function.
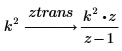
2. Use the keyword expand to expand the result.
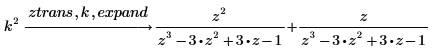
3. Use the keyword laplace to find the Laplace transform of a function.
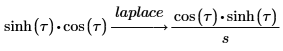
4. Use the keyword simplify to get the result in a simplified form.
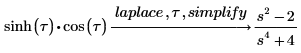
5. Find the inverse Fourier transforms of functions sin and sinc and present the results in a simplified form.
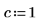
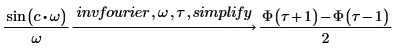
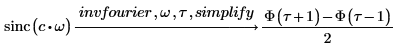
For input functions that have no symbolic transform, use the numerical dft function.
Fourier Transform Factorization
1. Add nfact and ofact alongwith fourier to the expression.
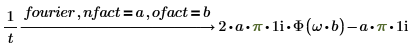
2. Add nfact and ofact alongwith invfourier to the expression.