Example: State Space Solver
Use the solver statespace to solve a state space representation of a system of first-order ordinary differential equations (ODEs).
Specifically, find the solution to the case of unforced harmonic oscillator in which the right-hand side of the harmonic oscillation equation is 0:
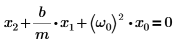
There are three cases for the solution - overdamped, critically damped, and underdamped. |
Overdamped Solution
1. Write the mathematical equation for the overdamped solution:
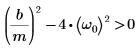
2. Define the initial conditions, the mass of the object, the damping constant, the start and end of the integration interval, and the number of points:
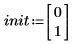
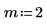
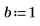
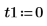
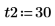
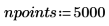
3. Set the natural, or resonant, frequency of the system.
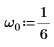
4. Verify that the condition of overdampness exists:
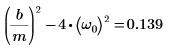
5. Write the ODE in matrix form:
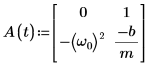
6. Call the statespace function:
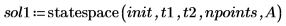
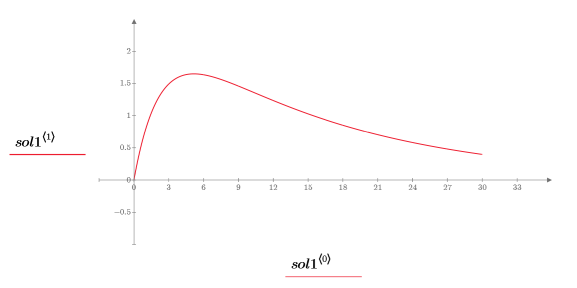
7. Plot the solution:
Critically Damped Solution
1. Set the natural, or resonant, frequency of the system.
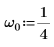
2. Verify that the condition of critical dampness exists:
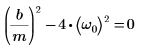
3. Write the ODE in matrix form:
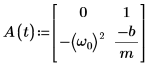
4. Call the statespace function:
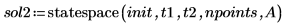
5. Plot the solution:
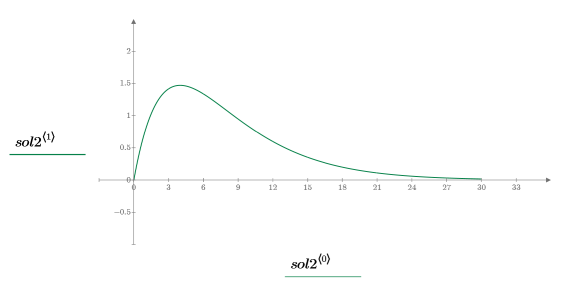
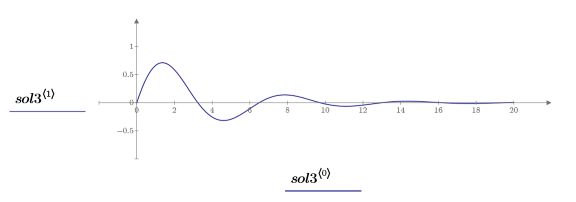
Underdamped Solution
1. Set the natural, or resonant, frequency of the system.
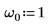
2. Verify that the condition of underdampness exists:
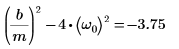
3. Write the ODE in matrix form:
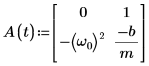
4. Call the statespace function:
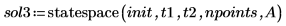
5. Plot the solution: