Example: Probability Density and Cumulative Probability Distribution
Use the dnorm, pnorm, cnorm, and qnorm functions to demonstrates the differences between various probability functions.
1. Define the mean and the standard deviation of a normal distribution.
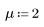
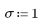
2. Plot the probability density (blue) and the cumulative probability (black and red) of normal distributions.
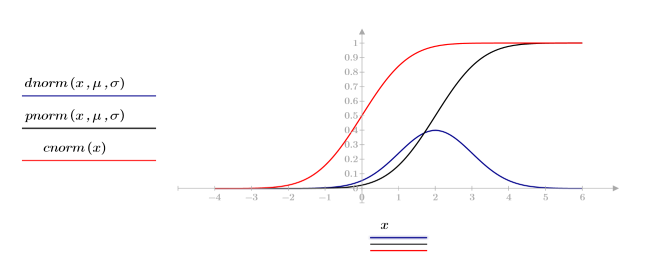
The dnorm function calculates the probability density at x of a normal distribution with mean μ and standard deviation σ. The pnorm function calculates the cumulative probability distribution of the normal distribution. The cnorm function is the cumulative probability distribution for the normal distribution with μ = 0 and σ = 1.
3. Use the qnorm function to calculate the value of x when the area under the curve, from - ∞ to x, is half the area under the whole curve.
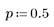
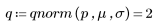
In this case, the value of x is equal to the mean, as confirmed by the following formula:
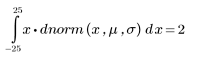
The probability density at q is easily recovered by using the pnorm function, which is the inverse of the qnorm function:
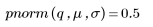
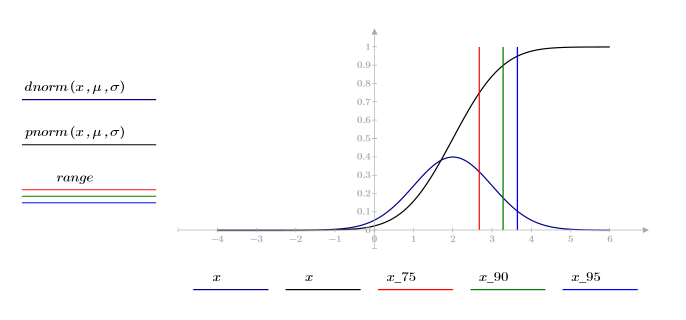
4. Use the qnorm function to find the 75th, 90th, and 95th percentiles of the normal distribution.
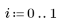
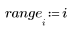
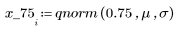
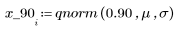
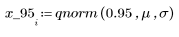
5. Plot the probability density (blue) and the cumulative probability (black) of a normal distribution, adding the percentiles calculated above (75%: red, 90%: green, 95%: blue).