Example: Cholesky Factorization of Real Matrices

Functions > Vector and Matrix > Matrix Factorization > Example: Cholesky Factorization of Real Matrices

Use the Cholesky function to perform Cholesky factorization of a real matrix.

To avoid logical mismatches when performing boolean comparisons, enable Approximate Equality in the Calculation Options drop-down list.

1. Define a real positive definite square matrix M.

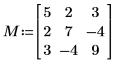
2. Apply the eigenvals function to ensure that the matrix is positive definite.

3. Apply the rank function to ensure that M is a full-rank matrix.

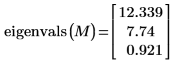
4. Set arguments p and u to control the enabling/disabling of pivoting and lower/upper factorization.

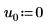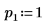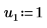5. Use the Cholesky function to perform the default factorization of matrix M - with pivoting and lower factorization.

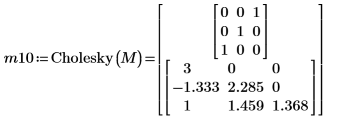
The default function Cholesky(M) is equivalent to Cholesky(M,1,0).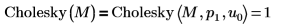

<region id="ID0ESM1EB" actualWidth="284.50666666666672" actualHeight="27.791200000000003" top="844.80000000000018" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="80">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </math>
</region>

6. Show that P10T x M x P10 = L10 x L10T.

<region id="ID0ERP1EB" actualWidth="165.17000000000002" actualHeight="62.800000000000004" top="940.80000000000018" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="82"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>0</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E6P1EB" actualWidth="260.32666666666665" actualHeight="62.800000000000004" top="1017.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="84"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>1</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>
<region id="ID0ESQ1EB" actualWidth="202.72666666666666" actualHeight="62.800000000000004" top="1094.4" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="86"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>	<region id="ID0EAR1EB" actualWidth="177.81666666666666" actualHeight="62.800000000000004" top="1094.4" left="307.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="88"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>
<region id="ID0ETR1EB" actualWidth="218.39000000000002" actualHeight="27.752000000000002" top="1152.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="90"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>

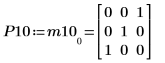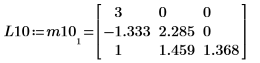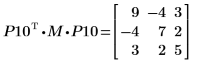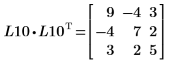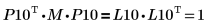The relationship is logically true.

7. Use the Cholesky function to perform factorization of matrix M - with no pivoting and lower factorization (default).

<region id="ID0EYT1EB" actualWidth="344.06666666666672" actualHeight="62.800000000000004" top="1305.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="92">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m00</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

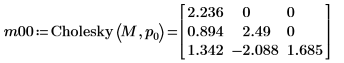
Not specifying argument u, as in Cholesky(M, 0), is equivalent to setting it to 0 as in Cholesky(M, 0, 0).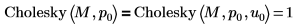

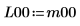
<region id="ID0ERV1EB" actualWidth="307.08666666666676" actualHeight="27.791200000000003" top="1401.6000000000001" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="94">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id xml:space="preserve">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

The returned lower matrix, L10, when pivoting is enabled is NOT equal to the returned lower matrix, L00, when pivoting is disabled.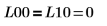

The relationship is logically false.

8. Show that M = L00 x L00T.

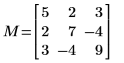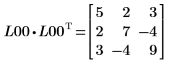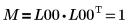The relationship is logically true.

9. Use the Cholesky function to perform factorization of matrix M - with pivoting and upper factorization.

<region id="ID0EU51EB" actualWidth="353.51333333333338" actualHeight="118.60000000000001" top="1881.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="106">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m11</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

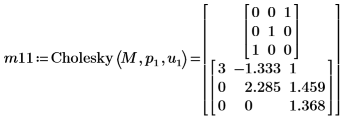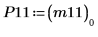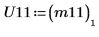10. Show that P11T x M x P11 = U11T x U11.

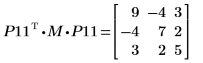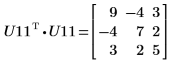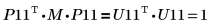The relationship is logically true.

11. Use the Cholesky function to perform factorization of matrix M - with no pivoting and upper factorization.

<region id="ID0E4F2EB" actualWidth="366.78000000000003" actualHeight="62.800000000000004" top="2304.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="118">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m01</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

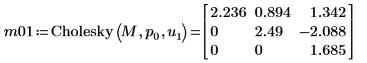
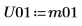
12. Show that M = U01T x U01.

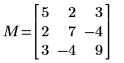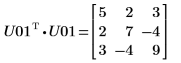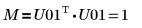The relationship is logically true.