Example: Least-Square Spline
Spline2, Binterp, and DWS
Use the Spline2 function to find the optimal set of knots that Binterp needs to compute a least-square spline interpolation.
1. Define a data set.

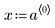 | 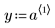 | 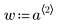 |
w is a vector of weights giving the estimated standard deviations of the random error in y.
2. Define the degree of the desired spline polynomials.
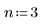
3. Call the Spline2 function.
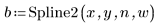

The first element of vector b is the B-spline order. The second element gives the number of intervals (knots - 1). The next elements are the knot values. The remaining elements contain the coefficients for the B-Spline basis functions.
The first and last knots, when automatically generated, match the endpoints of the original x-data:
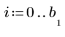
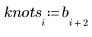
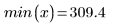 | 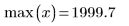 |
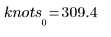 | 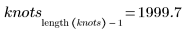 |
4. Call the Binterp function for a range of values that matches the range of x.
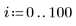
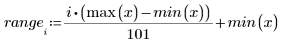

Row i of spline1 contains the interpolated value, and the first, second and third derivatives at the point defined in range i.
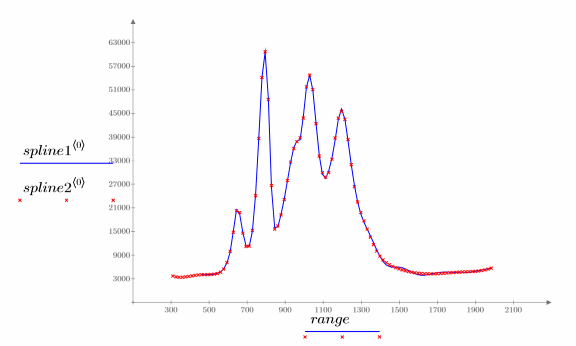
5. Plot the original data and the interpolated spline.
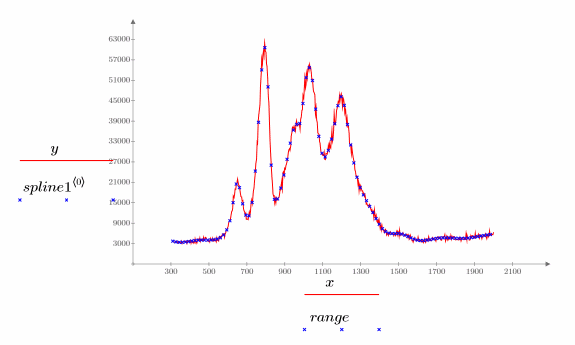
The optimal number of knots and their spacing are determined by the Durbin-Watson statistic. This statistic should be around 2 for a good fit. The statistic can be found by using the DWS function or by extracting the relevant element from matrix b:
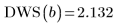
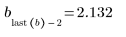
6. Use the optional last argument of Spline2, a percentage from 0 to 1, to provide a significance level, or reject level, for the Durbin-Watson test.
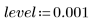
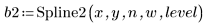
In general, although not always, higher reject levels produce more knots and longer calculations.
7. Calculate the number of knots used by Spline2.
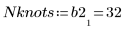
8. Call the DWS function to calculate the Durbin-Watson statistic.
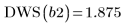
9. Plot the two interpolated splines.
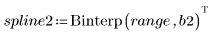
You can interpolate without weights:
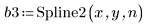
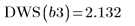
You can interpolate without weights, but with a reject level:
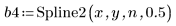
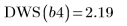
Spline Derivatives
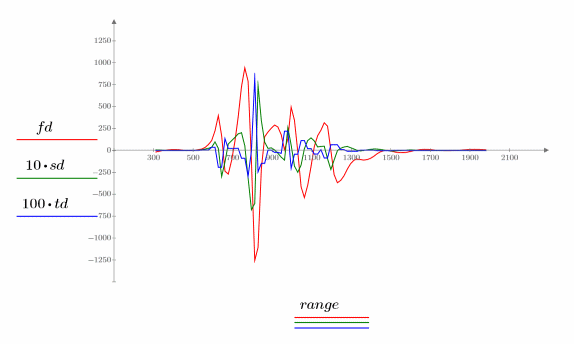
Plot the first three derivatives of the interpolation spline.
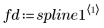
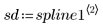
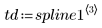
Supplying your own Knots
You can supply your own knots for the B-spline interpolation.
1. Define a string of knots.
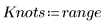
2. Plot the interpolated spline.
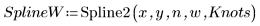
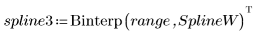
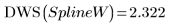
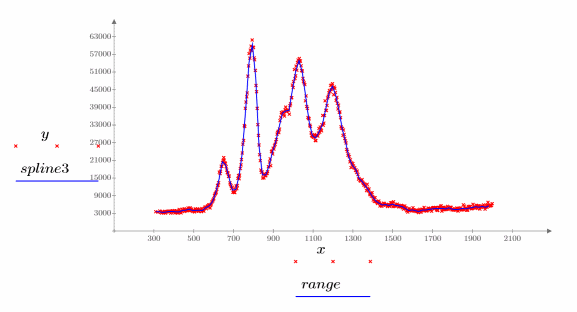
You can supply knots without a weighting vector:

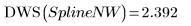
Outliers
You can see the effect of removing an outlier on the spline interpolation.
1. Call the GrubbsClassic function to detect the point which is the most likely to be an outlier.

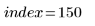
There is a suspicious point at the very top of the second data peak.
2. Remove the point from the data set and from the weighing function.
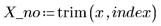
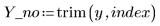
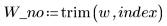
3. Call the Spline2 function for the new data set.
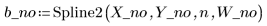
According to the Durbin-Watson statistic, the fit has improved:
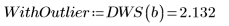
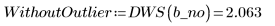
4. Compare the results of the interpolations at the suspicious data value:
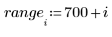
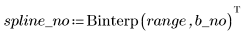
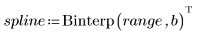
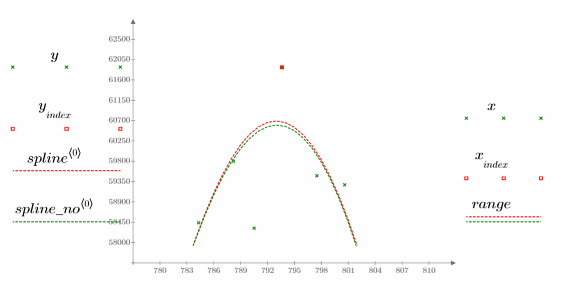
The spline drops slightly when the outlier is removed.