Example: Grayscale Morphology
Use the grayscale morphology functions for extracting image components. You can also describe object shapes by picking out small bright or dark features in an image.
For information on using this example, refer to About Image Processing Examples.
gray_erode
In binary erosion you use a structuring element to define a neighborhood around each pixel. In this pixel neighborhood the presence of any background pixels causes the foreground to become background. Grayscale erosion is an extension of this, where the structuring element's pixel values are subtracted from the input image's pixel values. The output is the minimum resulting pixel value within the boundary of the structuring element.
1. Create a 5 x 4 sequential matrix.
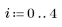
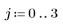
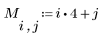
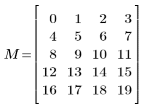
2. Create a simple structuring element (SE).
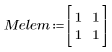
3. Use the gray_erode function to perform grayscale erosion with the origin of the SE at (0,0).
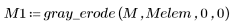
4. Evaluate the new matrix, which should be equal to M - 1 except at the rightmost column and bottommost row (boundary conditions).
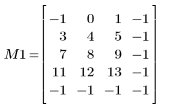
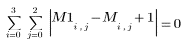
5. Use the READ_IMAGE function to read in an image.
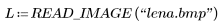
6. Erode a more realistic image with a 5 x 5 centered SE.
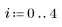
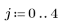
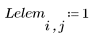
7. Apply the gray_erode function to the new image, and then use the WRITEBMP function to save it to a file..
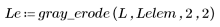
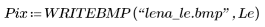
8. Display the original and eroded images.
 (lena.bmp) |  (lena_le.bmp) |
As expected, we notice that the image has darkened in general, the darker regions have expanded, and some brighter details have disappeared.
gray_dilate
In binary dilation, a structuring element is used to define a neighborhood around each pixel in which the presence of any foreground pixel causes the background to become foreground.
1. Use the same sequential matrix and structuring element (SE) as previously.
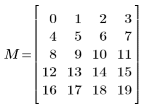
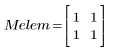
2. Use the gray_dilate function to perform grayscale dilation with the origin of the SE at (0,0).
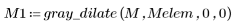
3. Evaluate the new matrix, which should be equal to M + 1 except the at the rightmost column and bottommost row (boundary conditions).
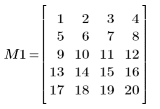
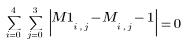
4. Apply the gray_dilate function to the previous image.
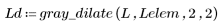
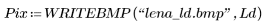
5. Display the original and dilated images.
 (lena.bmp) |  (lena_ld.bmp) |
The dilation results in an increased overall brightness, expanded bright regions, and loss of small dark details.
gray_open, gray_close
Grayscale opening and closing are defined in an analogous way to opening and closing in binary morphology; opening is grayscale erosion followed by grayscale dilation, and closing is grayscale dilation followed by grayscale erosion.
Apply gray_open and gray_close to the sequential matrix to see that they are equivalent to erosion and dilation combined.
1. Apply grayscale opening to the sequential matrix.
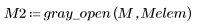
2. Apply grayscale erosion to the sequential matrix, with the origin of the SE at (0,0).
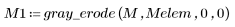
3. Apply grayscale dilation to the eroded matrix, with the origin of the SE at (0,0).
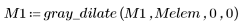
4. Show that grayscale opening is equivalent to combined grayscale erosion and dilation.
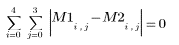
5. Apply grayscale closing to the sequential matrix.
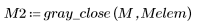
6. Apply grayscale dilation to the sequential matrix, with the origin of the SE at (0,0).
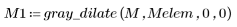
7. Apply grayscale erosion to the dilated matrix, with the origin of the SE at (0,0).
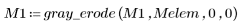
8. Show that grayscale closing is equivalent to combined grayscale dilation and erosion.
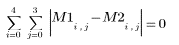
9. Apply the functions to the test image L, and compare the dilated, eroded, opened, and closed images.

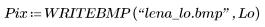

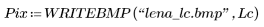
 (lena_ld.bmp) |  (lena_le.bmp) |
 (lena_lc.bmp) |  (lena_lo.bmp) |
Grayscale opening and closing result in no overall brightness change, while dilation and erosion change the brightness. Both dilation and closing enhance bright and reduce dark features in the image, while erosion and opening enhance dark and reduce bright features.