Example: Forward Transform dft
Use the dft function to find the complex Fourier transform of a real or complex-valued vector or matrix of any size, with constant time or space between samples.
1-D Complex Sinusoidal Data
Create a simulated complex data set with N data points at sample spacing T.
1. Define the number of data points.
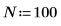
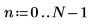
2. Define time T at which samples are collected.
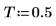
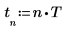
3. Set the angular frequency.
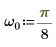
4. Use the exp function to define an exponential function.
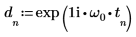
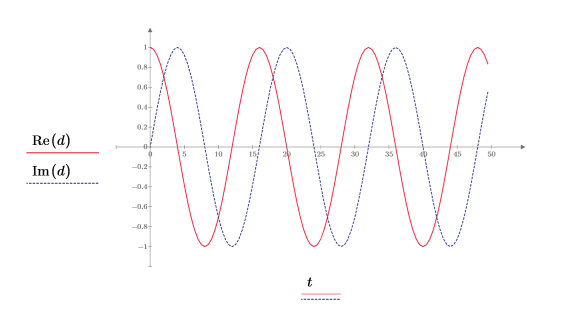
5. Use the Re and Im functions to extract and plot the real and imaginary components as functions of time.
6. Apply the dft function to transform the data to the frequency domain.
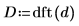
7. Collect the absolute values of D into a new array.
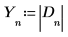
8. Define the sampling frequency and the frequency corresponding to the nth entry in the transformed vector.
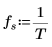
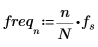
9. Use the match and max functions to find the peak and the corresponding frequency within the transformed signal.
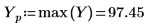
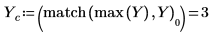
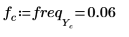
10. Plot the transformed vector and use vertical and horizontal markers to mark the frequency at which the amplitude is at its maximum.
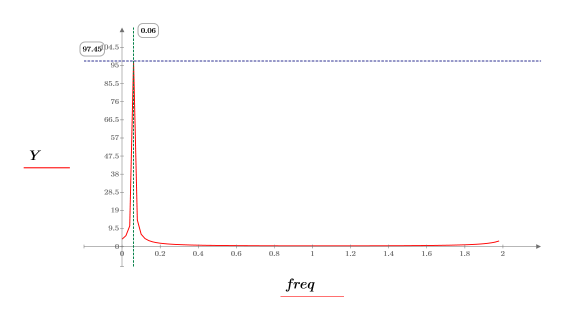
◦ The upper half of the frequency-domain samples represent the negative frequencies.
◦ This complex signal has no negative frequency content.
Additional Information
• For a real data vector v, the vector dft(v) is, in general, complex and conjugate symmetric about the middle value. In the case of a real matrix, each column of the result is conjugate symmetric.
• For any square array input A, dft(A) is symmetric.
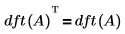
• According to the Nyquist sampling theorem, the sampling frequency must be at least twice the highest frequency you wish resolved by the Fourier transform.
• The prime number divisor algorithm used in the Fast Fourier Transform slows down when the number of data points is a large prime number. You may never encounter this problem, but do bear this in mind if you need to work with very large prime numbers of data points.