Example: Filtering in the Fourier Transform Domain
Use the funconv, matconv, funcdeconv, and matdeconv functions to convolve or deconvolve an image with a function, f, or mask, E, by multiplying the two together in spatial frequency (the Fourier transform domain). Filtering in the frequency domain can result in a variety of smoothing, edge detection, and periodic noise-reduction operations, depending upon the chosen function or mask. It is often mathematically more efficient to filter in the transform domain, or easier to define filters, than by using convolution in the image domain.
For information on using this example, refer to About Image Processing Examples.
funconv
Use this function to filter an image M with a function in spatial frequency. The real-valued function, f, is used to construct a mask, N, the same size as M. M is Fourier-transformed, and then multiplied termwise by the mask.
The mask is constructed by passing arguments to f which are the normalized distance from the upper-left corner of M. This process continues to the center of the mask, at which point the mask is duplicated in four pieces symmetrically. This process is used because the upper-left corner is DC (zero frequency).
1. Start to construct a mask by defining the image matrix M.
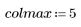
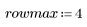
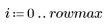
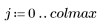
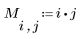
2. Find the pixel that represents the center of the image matrix.
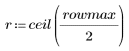
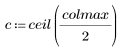
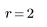
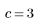
3. Create new range variables representing the values from the upper-left corner to the image center.
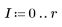
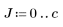
4. Use the defined range variables and a masking function to create the upper-left quadrant of the mask.
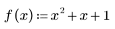
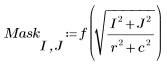
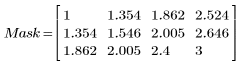
The (0, 0) entry is f(0), and the (r, c) entry is f(1).
The mask is constructed by passing arguments (the normalized distance from the upper-left corner of M) to f. This process continues to the center of the mask, at which point the mask is duplicated in four pieces symmetrically. This process is used because the upper-left corner is DC (zero frequency).
5. Construct the rest of the mask matrix using funconv.
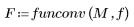

If the convolution expands the image scale, you can scale the output matrix to the [0, 255] range.
funcdeconv
This deconvolution function takes a frequency-domain image and a frequency-domain function and deconvolves them.
The last argument of funcdeconv e is a small term that is added to the denominators of all the expressions during the routine. As a starting point, type a value of 0 for e. If a divide-by-zero error message appears, type a small value for e.
1. Call the funcdeconv function.
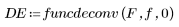
2. Evaluate DE to view the result of funcdeconv and compare with the original matrix.


matconv
The matconv functions performs the same frequency-domain multiplication and transforms as funconv, but it accepts a mask as an input instead of a function. The mask must be of the same size as the original image. You only supply the upper-left quadrant of the mask.
1. Read in a sample image.
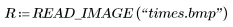
2. Count the number of rows and columns in the image matrix.
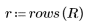
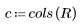
3. Define the dimensions of a mask.
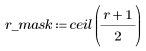
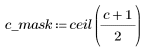
4. Define the mask C.
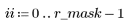
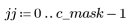
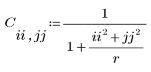
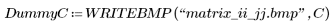
You can try the following highpass filter for C: 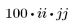 |
5. Apply matconv to R and C.
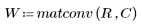
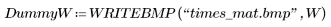
R | C | W |
|---|---|---|
 (times.bmp) |  (matrix_ii_jj.bmp) |  (times_mat.bmp) |
matdeconv
Use matdeconv to recover the original image. Because deconvolution potentially involves division by elements with zero intensity, e is added to the denominator of each division to eliminate this problem.
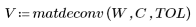
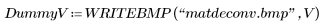

(matdeconv.bmp)
You can experiment with other filter functions, keeping in mind that the upper-left corner of the mask corresponds to low frequencies, and the lower-right corner corresponds to high frequencies. Try different images.