Example: Filtering an Image
Demonstrate filtering in the Fourier transform domain in two dimensions by convolving a two-dimensional image with a window using inverse DFT. The filter is a square aperture, a lowpass filter.
1. Define the dimensions and elements of an image matrix.
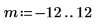
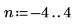
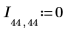
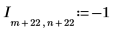
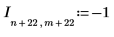
2. Use the scale function to scale the image.
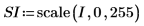
3. Use the WRITEBMP function to write the image to an external file.
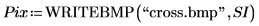
4. Browse for the written file and insert the image.

(cross.bmp)
5. Define the dimensions of the aperture.
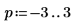
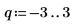
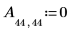
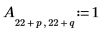
6. Use the scale function to scale the aperture, then write the image to an external file.
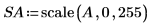
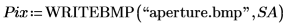
7. Browse for the written file and insert the image of the aperture.

(aperture.bmp)
The 2D boxcar transforms to a 2D sinc function, with most of its frequency content in the low frequencies (in the center), which makes it an adequate lowpass filter.
8. To convolve the aperture with the image, use the dft function to transform both, multiply the transforms elementwise using the vectorize operator, and then use the idft function to take the inverse transform.
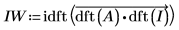
9. Use the center function to ensure that the DC component of the image is in the center.
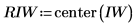
10. Turn the elements of the matrix into real numbers.
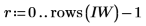
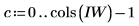
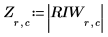
11. Use the scale function to scale the image.
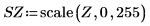
12. Use the invertimage function to invert the image.
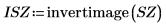
13. Use the WRITEBMP function to write the image to an external file.
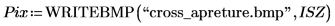
14. Browse for the written file and insert the image of the cross.

(cross_aperture.bmp)
The new image lost its high-frequency content, that is, its sharp edges.
15. Reverse the process by deconvolution, which is achieved by dividing the image transform elementwise by the aperture transform (a small amount is added to each element of the aperture to make sure there is no division by 0).
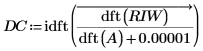
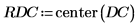
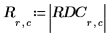
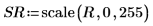
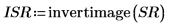
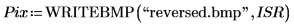
16. Browse for the written file and insert the image of the cross.

(reversed.bmp)
The image regained its high-frequency content, that is, its sharp edges.