Example: Discrete Cosine Transform

Functions > Image Processing > Transform Domain > Example: Discrete Cosine Transform

Use the dct and idct functions to calculate the discrete cosine transform and the inverse transform, respectively. This transform has the advantage of concentrating most of the image "energy," or information, in a few frequency components, making a good choice for encoding.

For information on using this example, refer to About Image Processing Examples.

1. Define a matrix M of size N x P.

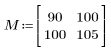
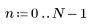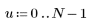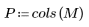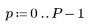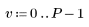2. The implementation of the cosine transform uses the type II DCT. Define DCT to be an analytic formula for this transform.

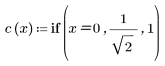
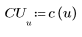
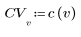
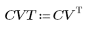
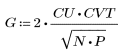
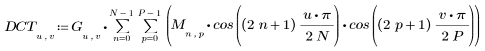
3. Evaluate matrix DCT.

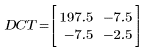
4. Apply function dct to matrix M.

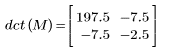
5. Calculate the maximum error between DCT and the dct function.

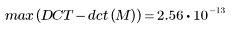
Energy Compaction

The cosine transform has very good energy-compaction properties, which means that it concentrates most of the energy in the first few coefficients of the transform.

1. Define an input matrix.

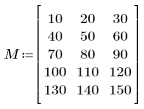
2. Apply the dct function to matrix M and evaluate it.

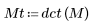
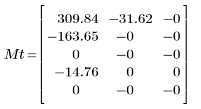
The resulting matrix shows that most of the energy, which is related to the coefficient values, is concentrated in the first few elements.

idct

The inverse function is used to recover an original image from its transform.

1. Read in a black-and-white version of the Mona Lisa.

(mona.bmp)

2. Apply the dct function to transform the image.

(mona_noise.bmp)

3. Apply the inverse function to recover the image.

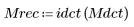
(mona_rec.bmp)

4. Verify the energy-compaction property of the DCT by looking at histograms of the transformed and original images.

<region id="ID0EL64Y" top="3000" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">H</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">Horig</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

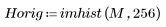
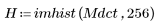
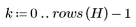
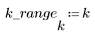
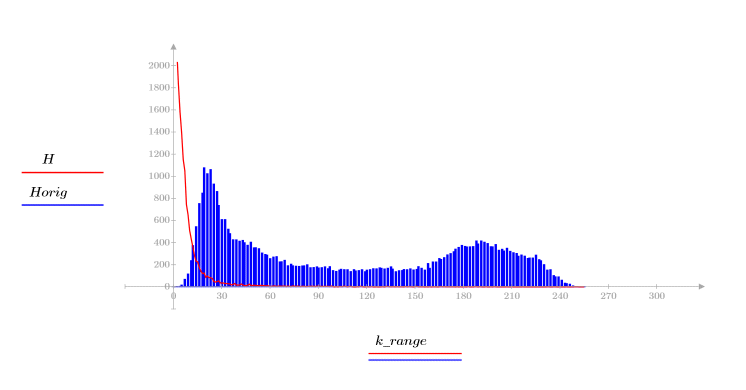
The transformed image concentrates most of the energy in the first few bins of the histogram, while the distribution of the original image is spread out. This makes the transformed image a better candidate for encoding or transmission, since most of the image information can be relayed with very few frequency components. For this reason the DCT is used for image compression.