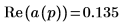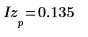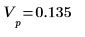Example: dft and idft of a Vector
Use the dft and idft functions for finding the forward or inverse Discrete Fourier Transform of a vector.
1. Define the length of a data vector.
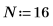
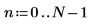
2. Use the exp function to create a real data vector of length N.
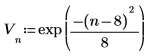
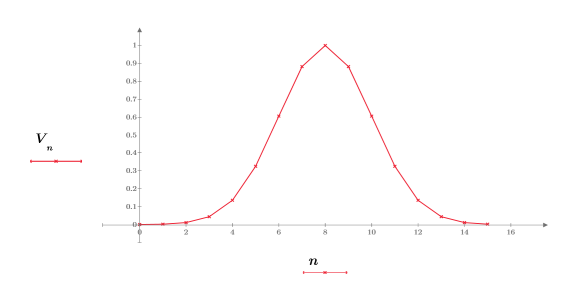
3. Plot the data.
4. Use the dft function to calculate the Discrete Fourier Transform of V.
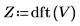
5. Plot the absolute values of Z.
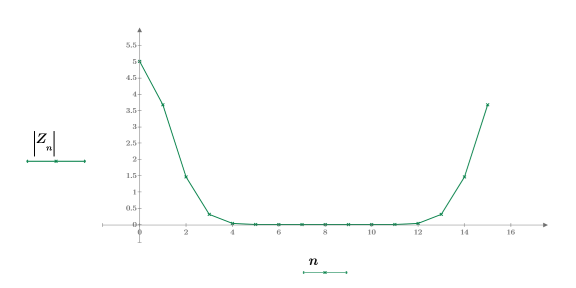
6. Show the definition of the dft function.
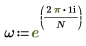
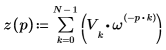
7. Use the above definition to find a specific frequency element and compare it with the corresponding element in the output of the dft function.
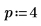
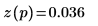
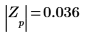
Gaussian idft
The idft function is the inverse transform of dft. It accepts a real or complex vector as its argument and returns a vector of the same length.
1. Show that the inverse transform of a dft function is the function itself.
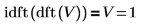
2. Use the previously defined vector V, then show that the inverse of the dft of V is V itself.
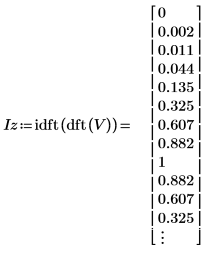 |  |
3. Show the definition of idft function.
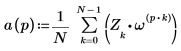
4. Use the above definition to find a specific frequency element and compare it with the corresponding element in the output of the idft function and vector V.