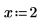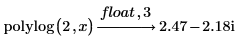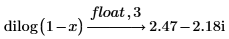Example: Demonstrating Symbolic Functions

Functions > Symbolic Functions > Example: Demonstrating Symbolic Functions

This example demonstrate the beta and zeta functions, the digamma and polygamma Psi functions, and the dilog and polylog functions. Use the keyword float with the symbolic evaluation operator to evaluate functions numerically.

The beta and zeta Functions

1. Note the following integral of sin, which is symbolically evaluated to the beta function.

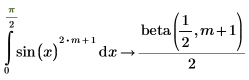
2. Evaluate the beta function when m = 2.

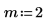
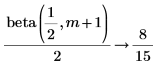
3. Note the following integral and series, which is symbolically evaluated to the zeta function.

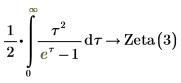
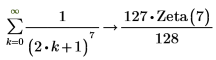
4. Evaluate the zeta function for z = 2 and z = 5.

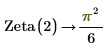
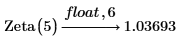
The Digamma and Polygamma Functions

1. Evaluate the digamma function Psi when x = 1 and x = 2.

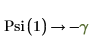
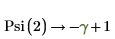
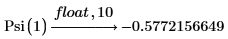
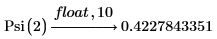
In the above examples, γ is Euler's constant.

2. Evaluate the polygamma function Psi when z = 1, k = 1 and k = 2.

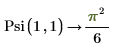
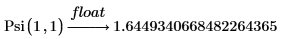
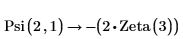
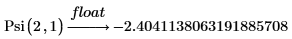
The dilog and polylog Functions

1. Evaluate the dilog function when x = 2.

<region id="ID0ENWDCB" actualWidth="120.71666666666668" actualHeight="51.158666666666669" top="1113.6000000000001" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="41">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">dilog</id>
        <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <neg />
            <apply>
              <pow />
              <id xml:space="preserve" labels="CONSTANT">π</id>
              <real>2</real>
            </apply>
          </apply>
          <real>12</real>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

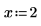
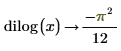
2. Evaluate the dilog function when x = 2.0.

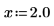
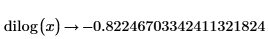
3. Limit the result to 10 significant places.

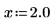
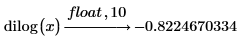
4. Note the following integral, which is symbolically evaluated to the polylog function. The polylog function appears in the result of the following integral.

<region id="ID0EJ3DCB" actualWidth="360.45333333333338" actualHeight="80.552" top="1382.4" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="46">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">τ</id>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">e</id>
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">τ</id>
              </apply>
              <real>1</real>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <id xml:space="preserve" labels="FUNCTION">polylog</id>
            <sequence>
              <real>2</real>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <id xml:space="preserve" labels="VARIABLE">τ</id>
              </apply>
            </sequence>
          </apply>
          <parens>
            <apply>
              <minus />
              <apply>
                <mult />
                <id xml:space="preserve" labels="VARIABLE">τ</id>
                <apply>
                  <id xml:space="preserve" labels="FUNCTION">ln</id>
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="CONSTANT">e</id>
                        <id xml:space="preserve" labels="VARIABLE">τ</id>
                      </apply>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <div />
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">τ</id>
                  <real>2</real>
                </apply>
                <real>2</real>
              </apply>
            </apply>
          </parens>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

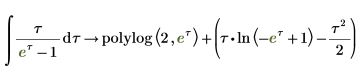
5. Evaluate polylog and dilog when x = 2.

<region id="ID0EB6DCB" actualWidth="228.85000000000002" actualHeight="39.2" top="1555.2000000000003" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="49">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">dilog</id>
        <apply>
          <minus />
          <real>1</real>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
        </apply>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">float</id>
          <real>3</real>
        </sequence>
      </command>
      <symResult>
        <apply>
          <minus />
          <real>2.47</real>
          <imag symbol="i">2.18</imag>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>